Imagine you are shopping on Amazon.com for some good weight lifting equipment. The equipment you want has blocks of many different weights that you can combine to lift.
The listing on Amazon gives you an array, blocks, that consists of n different weighted blocks, in kilograms. There are no two blocks with the same weight. The element blocks[i] denotes the weight of the ith block from the top of the stack. You consider weight lifting equipment to be good if the block at the top is the lightest, and the block at the bottom is the heaviest.
More formally, the equipment with array blocks will be called good weight lifting equipment if it satisfies the following conditions (assuming the index of the array starts from 1):
- blocks[1] < blocks[i] for all (2 ≤ i ≤ n)
- blocks[i] < blocks[n] for all (1 ≤ i ≤ n-1)
In one move, you can swap the order of adjacent blocks. Find out the minimum number of moves required to form good weight lifting equipment.
Example
Let the blocks be in the order: blocks = [3, 2, 1]
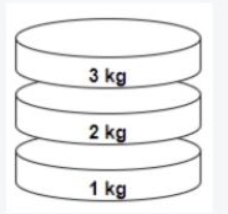
In the first move, we swap the first and the second blocks. After swapping, the order becomes:
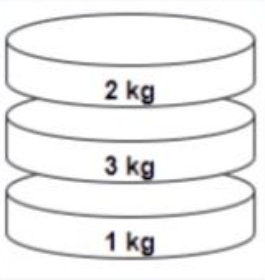
blocks = [2, 3, 1]
In the second move, we swap the second and the third blocks. After swapping, the order becomes:
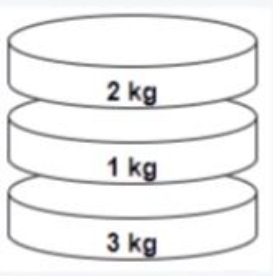
blocks = [2, 1, 3]
In the third move, we swap the first and the second blocks. After swapping, the order becomes:
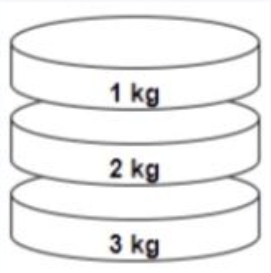
blocks = [1, 2, 3]
Now, the array satisfies the condition after 3 moves.
Function Description
Function Description Complete the function getMinNumMoves in the editor below.
getMinNumMoves has the following parameter: int blocks[n]: the distinct weights
Returns int: the minimum number of operations required
Constraints
- 2≤1052≤n≤105
- 1≤blocks≤1091≤blocks[i]≤109 for all 1≤1≤i≤n
- blocks consists of distinct integers.
Analysis:
In this coding challenge, the objective is to reorder an array of distinct integer weights to satisfy specific sorting conditions. We are given an array, blocks, where each element represents the weight of a block. The goal is to reorder the blocks so that the lightest block is at the beginning of the array (top of the stack) and the heaviest block is at the end (bottom of the stack).
To achieve this, we must follow the rules laid out in the problem statement:
blocks[1]should be less than all other weights in the array.- Each
blocks[i](where1 < i < n) should be less thanblocks[n]. - We can only swap adjacent elements to reorder the array.
Our task is to write a function, getMinNumMoves, that calculates the minimum number of adjacent swaps required to sort the array according to the rules.
The challenge comes with specific constraints:
- The number of blocks
nis between 2 and 100,000. - The weight of each block is between 1 and 1 billion and is a distinct integer.
Before jumping into coding, an analysis of the problem suggests that this can be seen as a variant of the bubble sort problem, where we are interested in counting the swaps rather than actually sorting the array. However, given the potential size of the array, a naïve bubble sort approach would be inefficient and likely exceed the time limits for large inputs. We must therefore seek a more efficient method.
One approach is to first identify the positions of the lightest and the heaviest blocks. Since we can only perform adjacent swaps, the minimum number of moves required would be the sum of the moves to bring the lightest block to the beginning and the heaviest to the end. This can be achieved in a single pass from both ends of the array.
In summary, we will develop a solution that first identifies the target positions of the lightest and heaviest blocks, then calculates the minimum number of swaps needed to achieve the 'good weight lifting equipment' configuration.
在这个编程挑战中,目标是重新排序一个包含不同整数重量的数组,以满足特定的排序条件。我们被给定一个数组 blocks,其中每个元素代表一个块的重量。目标是重新排列这些块,使最轻的块在数组的开头(堆栈的顶部),最重的块在末尾(堆栈的底部)。
为了实现这一点,我们必须遵循问题陈述中列出的规则:
blocks[1]应该小于数组中的所有其他重量。- 每个
blocks[i](其中1 < i < n)应该小于blocks[n]。 - 我们只能交换相邻元素来重新排序数组。
我们的任务是编写一个函数 getMinNumMoves,该函数计算按照规则对数组排序所需的最少相邻交换次数。
挑战伴随着特定的限制:
- 块的数量
n在2到100,000之间。 - 每个块的重量在1到10亿之间,且为不同的整数。
在直接跳入编码之前,对问题的分析表明,这可以看作是冒泡排序问题的一个变体,在这里我们对计算交换次数感兴趣,而不是实际排序数组。然而,鉴于数组可能的大小,采用朴素的冒泡排序方法将是低效的,并可能会超过大输入的时间限制。因此,我们必须寻求更有效的方法。
一种方法是首先确定最轻和最重块的位置。因为我们只能执行相邻交换,所以所需的最小移动次数将是将最轻块移到开头和最重块移到末尾的移动次数之和。这可以通过从数组的两端进行单次遍历来实现。
总结来说,我们将开发一个解决方案,该解决方案首先确定最轻和最重块的目标位置,然后计算实现“好的举重设备”配置所需的最少交换次数。
OA代做,仅需359美元。
If you're afraid that you can't solve the OA on your own, please scan the code to contact me or telegram。
It's a paid service will cost you 359usd.Make sure you can get the perfect score.