5. New Algorithm

ByteDance is developing a new algorithm to implement in an upcoming software. The algorithm runs on a sequence of integers. Given an array data of size n, where the value of the i^th integer is represented by the array data[i], the algorithm will run on data as:

• For every integer k, where 1 ≤ k ≤ n. The algorithm will return the minimum common integer that occurs in all of the subarrays of the array data having length k.
• If there is no common integer occurring in any subarray of length k, then the algorithm will return -1.

Note:

• A subarray is a contiguous sequence of elements within an array.

Given an integer n, and an array data, find the array that the algorithm will return after running on data.

Example: Given, n = 5, data = [4, 3, 3, 4, 2].

k	subarrays	Minimum common integer
1	[4], [3], [3], [4], [2]	-1
2	[4, 3], [3, 3], [3, 4], [4, 2]	-1
3	[4, 3, 3], [3, 3, 4], [3, 4, 2]	3
4	[4, 3, 3, 4], [3, 3, 4, 2]	3

Hence, the algorithm will return the array [-1, -1, 3, 3, 2] after running on data.

Function Description

Complete the function minimumCommonInteger in the editor below. minimumCommonInteger has the following parameter:

• int data[n]: an array of integers.

Constraints

• 2 ≤ n ≤ 2*10^5
• 1 ≤ data[i] ≤ n

Input Format For Custom Testing

The first line contains an integer, n, denoting the number of elements in data. Each of the next n lines contains an integer data[i].

题解 | Solution:

对于每一个 k (1 <= k <= n)，我们需要找到长度为 k 的所有子数组，并检查这些子数组中的共同数字。若有共同数字，我们应选取其中的最小值；若没有共同数字，则返回 -1。

首先，我们可以采用滑动窗口的方法来遍历所有长度为 k 的子数组。每当窗口滑动时，我们可以使用哈希表来记录当前窗口内的数字出现的频次。然后，检查这些频次，寻找出现在所有子数组中的数字，并从中选取最小的一个。

这样的方法确保了我们只需遍历一次原数组，大大提高了效率。

For each k (1 <= k <= n), we need to find all subarrays of length k and check for common numbers in these subarrays. If there are common numbers, we should select the smallest one; if there are no common numbers, return -1.

First, we can use the sliding window method to traverse all subarrays of length k. Whenever the window slides, we can use a hashmap to record the frequency of numbers in the current window. Then, we check these frequencies, looking for numbers that appear in all subarrays and selecting the smallest one.

This method ensures that we only need to traverse the original array once, greatly improving efficiency.

伪代码 | Pseudocode:

another 5. DFS Algorithm

An implementation of the DFS (depth-first search) algorithm does not keep track of visited nodes and can potentially run into an infinite loop or exceed the recursion depth. Modify the implementation to include a mechanism for storing visited nodes, ensuring that each node is visited only once during the traversal. The solution must overcome the problems of infinite loops and recursion depth limits caused by revisiting nodes.

Write a function dfsWithVisitedLookup(graph, start) that takes in the following parameters:

• graph: A dictionary that represents the graph as an adjacency list. The keys of the dictionary are the nodes, and the values are lists of neighboring nodes.
• start: The node from which the DFS traversal begins.

The function should return a list of nodes visited during the traversal in the order they were visited.

Example:

pythonCopy code

graph = { 'A': ['B', 'C'], 'B': ['D', 'E'], 'C': ['F'], 'D': [], 'E': [], 'F': [] }

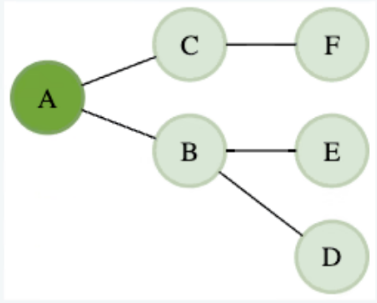
pythonCopy code

print(dfsWithVisitedLookup(graph, 'A'))

Output:

['A', 'B', 'D', 'E', 'C', 'F']

The graph has six nodes (A, B, C, D, E, F). Starting from node 'A', the DFS traversal visits the nodes in the order A → B → D → E → C → F. The modified algorithm should ensure that no node is revisited during the traversal.

Function Description:

Complete the function dfsWithVisitedLookup in the editor below.

dfsWithVisitedLookup has the following parameters(s):

• int start: the traversal start node
• int graph_nodes: the number of nodes
• int graph_from[m]: one end of each connection
• int graph_to[m]: the other end of each connection

此实现的DFS（深度优先搜索）算法没有跟踪已访问的节点，可能会进入无限循环或超出递归深度。您需要修改实现，以包含用于存储已访问节点的机制，确保在遍历过程中每个节点只访问一次。解决方案必须克服由于重新访问节点而导致的无限循环和递归深度限制问题。

The given DFS (depth-first search) implementation does not track the visited nodes, which could potentially result in an infinite loop or exceeding the recursion depth. You are required to modify the implementation to incorporate a mechanism to store the visited nodes. This ensures that each node is visited only once during the traversal. The solution should address the challenges of infinite loops and recursion depth limits caused by revisiting nodes.

Initialize an empty list called path to store the order of visits
Initialize an adjacency list called adj to store neighbors for each node

Define a function dfs(u):
Append u to path
For each neighbor v of u:
If v is not visited:
Call dfs(v)

Define a function dfsWithVisitedLookup(graph, start):
Get the length of graph and store as n
Initialize adj as an empty list of size n x n
For each (from, to) pair in graph:
Add to to the neighbor list of from
Initialize path as an empty list
Call dfs(start)
Return path

如果OA不会做，可以联系我们提供帮助