Code Question 1: Parentheses Perfection Kit

Description:
At Amazon, a user owns a unique tool called the "Parentheses Perfection Kit." This kit contains different types of parentheses, each with a specific efficiency rating. The goal is to create a balanced sequence of parentheses by adding zero or more parentheses from the kit to maximize the sequence's total EfficiencyScore.

The EfficiencyScore of a sequence is the sum of the efficiency ratings of the parentheses used from the kit.

A sequence is considered balanced if:

• It has an equal number of opening '(' and closing ')' parentheses.
• Each opening parenthesis is properly matched with a closing one in the correct order.

You are given:

• An initial parentheses sequence represented by the string s.
• A "Parentheses Perfection Kit" containing different types of parentheses in the form of the string kitParentheses.
• Efficiency ratings in the array efficiencyRatings.

Your task is to determine the maximum possible EfficiencyScore for a balanced sequence.

Example:

s = "()"  
kitParentheses = "()()"  
efficiencyRatings = [3, 4, -2, -3]  

Explanation:

• Initial sequence s is already balanced with an EfficiencyScore of 0.
• From the parentheses kit, adding:
  1. The first parenthesis '(' from the kit and pairing it with the first ')' results in a balanced sequence "()()", with EfficiencyScore = 3 + 4 = 7.
  2. Adding any other parentheses would lead to an unbalanced sequence or lower EfficiencyScore.

Sample Input for Custom Testing:

STDIN  
s = "()"  
kitParentheses = "()()"  
efficiencyRatings = [3, 4, -2, -3]

Sample Output:

7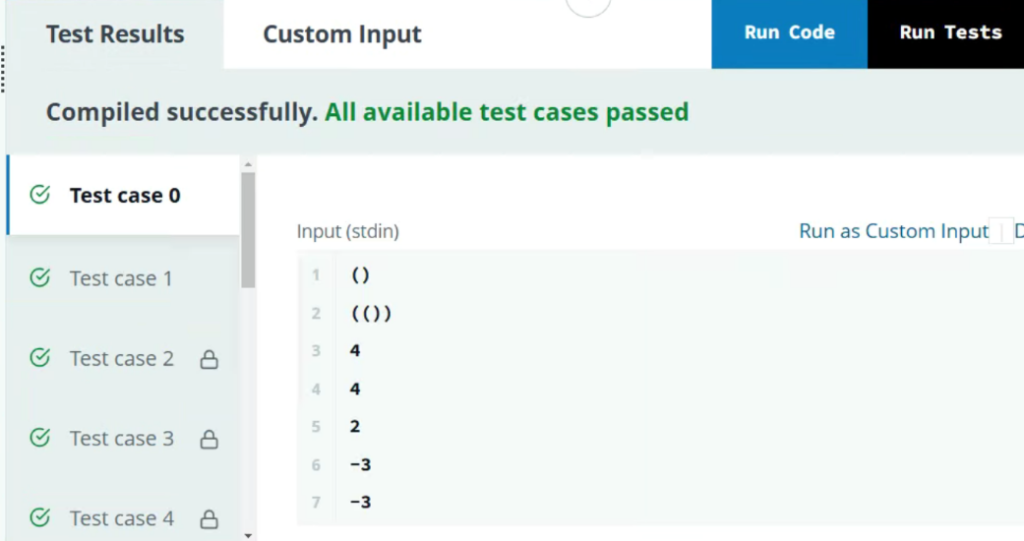

Code Question 2: Logistics Network Optimization

Description:
In Amazon's logistics network, optimizing package routing is crucial. The network consists of warehouses with specific storage capacities, and each warehouse connects to hubs to optimize inventory routing.

You are given:

• The storage capacities of warehouses in a non-decreasing order.
• Queries where two high-performance hubs are added at specific locations.

Your task: For each query, calculate the minimum total connection cost for all warehouses to connect to the nearest available hubs or the central hub at the last warehouse.

Example:

n = 6  
warehouseCapacity = [2, 5, 9, 12, 18]  
queries = [[2, 5], [1, 3]]  

Explanation:

• Initial Setup: Only a central hub is available at the last warehouse. The total connection cost is 18 - 2 + 18 - 5 + 18 - 9 + 18 - 12 + 18 - 18 = 62.
• Query 1 (Add hubs at positions 2 and 5):
  • 1st warehouse connects to hub at position 2: Cost = 5 - 2 = 3.
  • 2nd warehouse connects to hub at position 2: Cost = 5 - 5 = 0.
  • 3rd warehouse connects to hub at position 5: Cost = 9 - 5 = 4.
  • 4th warehouse connects to hub at position 5: Cost = 12 - 5 = 7.
  • 5th warehouse connects to itself: Cost = 18 - 18 = 0.
  • Total connection cost = 3 + 0 + 4 + 7 + 0 = 14.
• Query 2 (Add hubs at positions 1 and 3):
  • 1st warehouse connects to hub at position 1: Cost = 2 - 2 = 0.
  • 2nd warehouse connects to hub at position 3: Cost = 5 - 3 = 2.
  • 3rd warehouse connects to hub at position 3: Cost = 9 - 3 = 6.
  • 4th warehouse connects to hub at position 3: Cost = 12 - 3 = 9.
  • 5th warehouse connects to itself: Cost = 18 - 18 = 0.
  • Total connection cost = 0 + 2 + 6 + 9 + 0 = 17.

Sample Input for Custom Testing:

STDIN  
n = 6  
warehouseCapacity = [2, 5, 9, 12, 18]  
queries = [[2, 5], [1, 3]]

Sample Output:

14  
17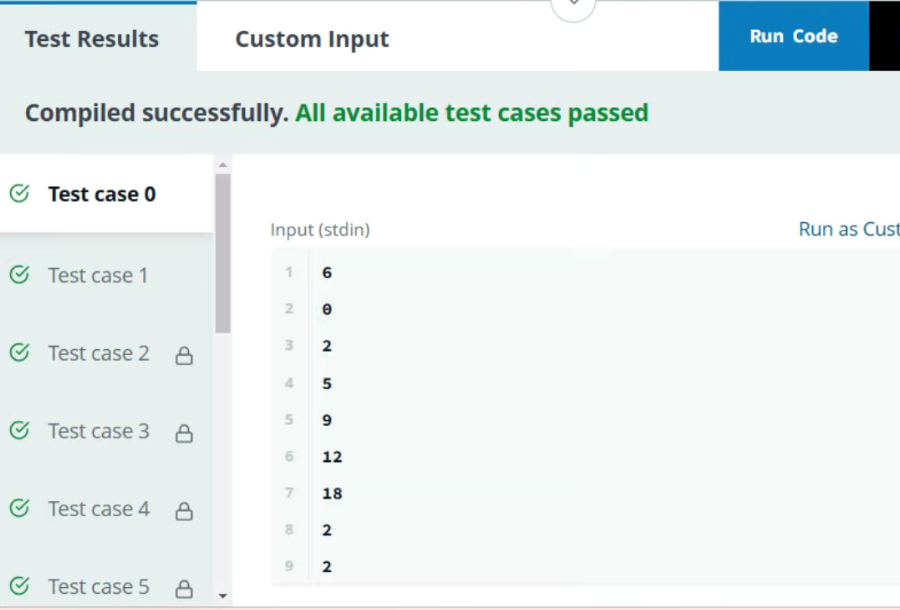

CSOAhelp长期稳定承接各大科技公司如TikTok、Google、Amazon等的OA笔试代写服务，确保满分通过。如有需求，请随时联系我们。

CSOAhelp consistently provide professional online assessment services for major tech companies like TikTok, Google, and Amazon, guaranteeing perfect scores. Feel free to contact us if you're interested.