在 Akuna Capital 这样的顶级交易公司,通过他们的严格筛选过程不仅需要有卓越的金融知识,还需要具备出色的算法和编程能力。最近,Akuna Capital 为候选人推出了一项极具挑战性的线上笔试(OA),旨在测试他们在高压环境下的算法思维和编码能力。这场限时 120 分钟的考核,将候选人推向极限,要求他们快速且准确地解决复杂问题。
Navigating the rigorous selection process of top trading firms like Akuna Capital requires not just financial acumen but also exceptional problem-solving skills. Recently, Akuna Capital rolled out a challenging Online Assessment (OA) for candidates, designed to test their algorithmic thinking and coding proficiency under pressure. This timed assessment, with a strict 120-minute limit, pushes candidates to the edge, requiring them to solve complex problems quickly and accurately.
1. Profitable Project Pairs
In a tech company, there are n projects available for the team to work on. Due to resource constraints, they can only work on any two of the projects. The expected profits for each project are provided in the array profit, while the implementation costs are given in the array implementationCost.
The task is to determine the number of pairs of projects that can be chosen from the available options such that the company earns a profit after implementing both projects. That is, two projects indexed i and j are chosen if:
(profit[i] - implementationCost[i]) + (profit[j] - implementationCost[j]) > 0
where 0 ≤ i < j < n.
Example
Given:
n = 5profit = [2, 3, 7, 1, 1]implementationCost = [3, 4, 5, 1, 2]
| Pair of Projects (0-based) | Net Profit from the First Project | Net Profit from the Second Project |
|---|---|---|
| [0, 2] | 2 - 3 = -1 | 7 - 5 = 2 |
| [1, 2] | 3 - 4 = -1 | 7 - 5 = 2 |
| [0, 3] | 7 - 5 = 2 | 1 - 1 = 0 |
| [2, 4] | 7 - 5 = 2 | 1 - 2 = -1 |
It can be seen that no other pair generates a net profit. Therefore, there are 4 profitable pairs that can be chosen from the given options.
Function Description
Complete the function getProfitablePairs in the editor below.
getProfitablePairs takes the following parameter(s):
int profit[n]: the profit earned by the company from each projectint implementationCost[n]: the cost of implementing each project
Returns:
long: the number of pairs of projects that are profitable
Constraints
1 ≤ n ≤ 10^51 ≤ profit[i], implementationCost[i] ≤ 10^9
Input Format For Custom Testing
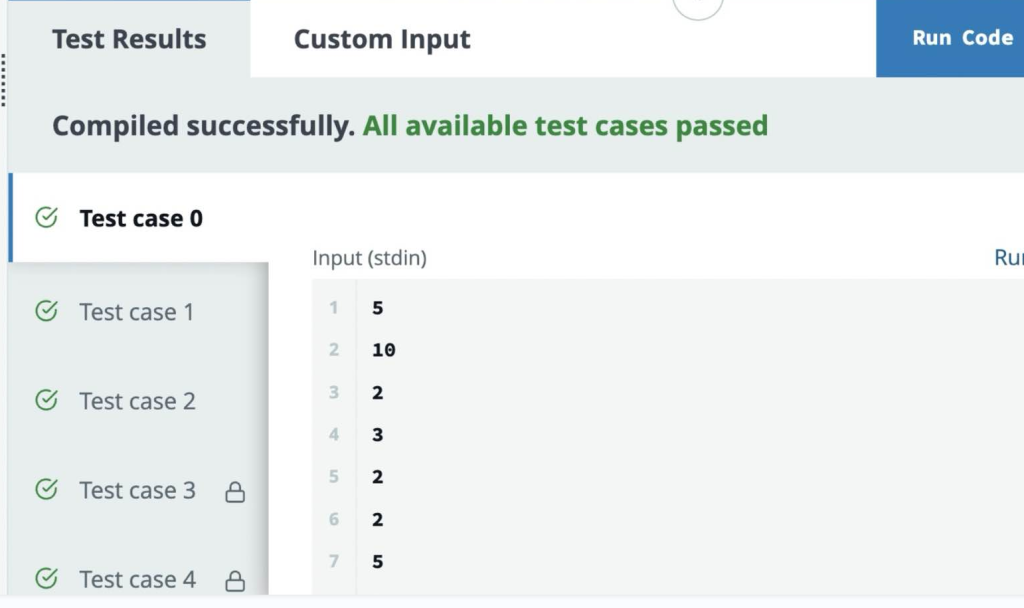
Sample Case 0:
Input
5
10 2 3 3 2
1 5 4 2
Output
5
Explanation:
The following pairs of projects are profitable:
- [0, 1]
- [0, 2]
- [0, 3]
- [0, 4]
- [1, 4]
2. Maximum Distinct
Consider two arrays a and b where each consists of n integers. In one operation:
- Select two indices
iandj(where 0 ≤ i, j < n). - Swap integers
a[i]andb[j].
This operation can be performed at most k times.
Find the maximum number of distinct elements that can be achieved in array a after at most k operations.
Example:
n = 5
a = [2, 3, 3, 2, 2]
b = [1, 3, 2, 4, 1]
k = 2
Steps:
- Select
i = 2,j = 0. Swapa[2]andb[0]. Now,a = [2, 3, 1, 2, 2]andb = [3, 3, 2, 4, 1]. - Select
i = 4,j = 3. Swapa[4]andb[3]. Now,a = [2, 3, 1, 2, 4]andb = [3, 3, 2, 2, 1].
Final result: a = [2, 3, 1, 2, 4] contains 4 distinct elements. There cannot be more than 4 distinct elements in array a.
Function Description:
You need to complete the function getMaximumDistinctCount in the code editor.
The function should take the following parameters:
int a[n]: an array of integers.int b[n]: an array of integers.int k: the maximum number of swap operations allowed.
Return:
- An integer representing the maximum number of distinct elements in
aafter at mostkoperations.
Constraints:
1 ≤ n, k ≤ 1000001 ≤ a[i], b[i] ≤ 1000000000
Problem 3: Star Sum
Problem Statement:
Given an integer k and graph G with g_nodes nodes and g_edges edges, find a star-graph. The value of a node i is given by values[i]. A 'k-star' is defined as a non-empty subgraph of G that is a star-graph and has at most k arms. A k-star graph with k given as 3, 4, 5, and 6 respectively, would look like this:
(Imagine visual of star graphs with different k values shown)
The goal is to return the sum of a k-star with the largest sum among all k-stars.
Example:
makefile复制代码g_nodes = 5
g_from = [3, 3, 3, 3]
g_to = [1, 2, 4, 5]
values = [10, 20, 30, 40, 50]
k = 2
Explanation: The graph is a star centered on node 3. The stars of k = 2 include node 3 as the center and any of the other two nodes as spokes. The largest sum k-star in this case includes nodes 3, 4, and 5, which sum to 30 + 40 + 50 = 120.
Function Description:
Complete the function bestSumKStar in the editor below.
The function has the following parameter(s):
int g_nodes: the number of nodes in the graph.int g_from[g_edges]: eachg_from[i]denotes the first endpoint of theith edge in the graph.int g_to[g_edges]: eachg_to[i]denotes the second endpoint of theith edge in the graph.int values[g_nodes]: eachvalues[i]denotes the value assigned to nodei.int k: the maximum number of arms in a star we are looking for.
Returns:
int: the largest sum of a non-emptyk-starin the graph.
Constraints:
- 2 ≤
g_nodes≤ 10⁵ - 1 ≤
g_edges≤ 10⁵ - 0 ≤
g_from,g_to≤ n-1 - 0 ≤
k≤ 10⁵ - -10³ ≤
values[i]≤ 10³, where 0 ≤ i < g_nodes - The graph does not contain any self-loops.
- The graph contains at most a single edge between a pair of vertices.
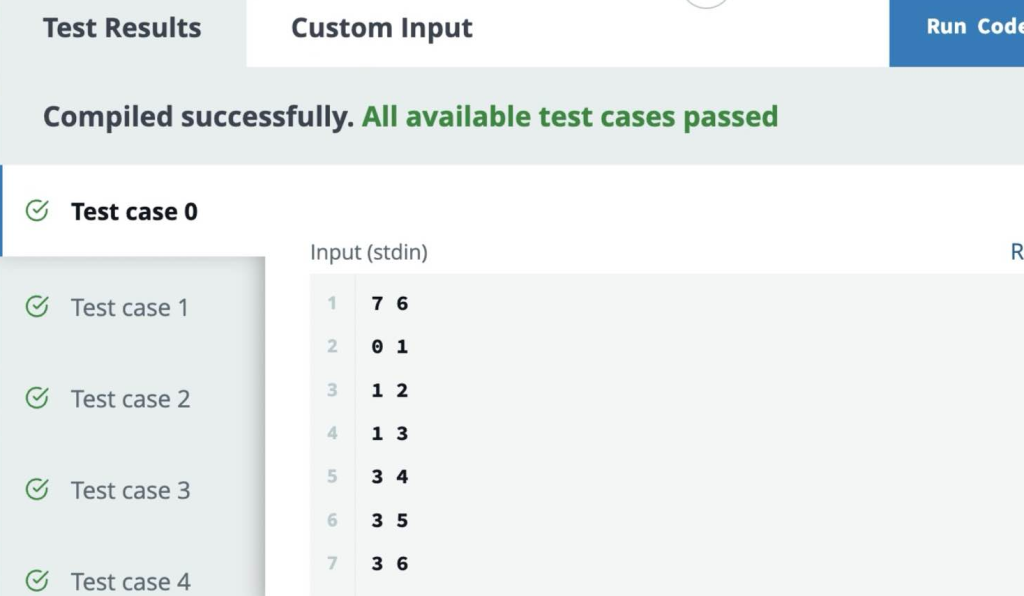
Sample Input for Custom Testing:
g_nodes = 7
g_edges = 6
g_from = [0, 1, 1, 3, 3, 3]
g_to = [1, 2, 3, 4, 5, 6]
values = [1, 2, 3, 4, 10, -10, -20]
k = 2
Sample Output:
16
Explanation: The star centered on node 3 with two arms connecting nodes 2 and 4 has the sum 4 + 2 + 10 = 16. This is the largest sum of any k-star (2-star in this case) that are sub-graphs of G.
If you are also worried about Online Assessment (OA) or simply don't want to go through the hassle of completing these tests on your own, we offer professional services to help you pass with flying colors. Our team has extensive experience and can provide you with one-on-one guidance and comprehensive solutions. Contact us and let's achieve success together!
我们提供面试辅助和 OA 代写服务,助您进入梦想大厂,欢迎随时咨询我。

