1. Code Question 1
A student is preparing for a test from Amazon Academy for a scholarship.
The student is required to completely read n chapters for the test where the iiith chapter has pages[i] number of pages. The chapters are read in increasing order of the index. Each day the student can either read till the end of a chapter or at most x pages, whichever is minimum. The number of pages remaining to read decreases by x in the latter case.
For example, if pages = [5, 3, 4] and x = 4:
- Day 1: The student reads 4 pages of the first chapter - pages remaining =
[1, 3, 4] - Day 2: The student can only read till the end of the first chapter - pages remaining =
[0, 3, 4] - Day 3: The student can read either till the end of the chapter or x=4x = 4x=4 pages, since 3 < 4, the student reads till the end of the chapter 2 - pages remaining =
[0, 0, 4] - Day 4: The student reads all the 4 pages of the last chapter - pages remaining =
[0, 0, 0]
The test will be given in days\text{days}days number of days from now. Find the minimum number of pages, xxx, which the student should read each day to finish all pages of all chapters within days\text{days}days number of days.
Function Description
Complete the function minimumNumberOfPages in the editor below.
minimumNumberOfPages has the following parameters:
int pages[n]: the number of pages in each chapterint days: the maximum number of days
Returns:
int: the minimum number of pages to be read each day, or -1 if it is not possible to finish
Constraints:
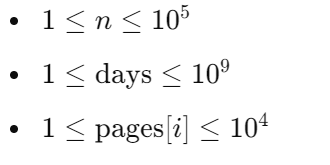
Sample Case 0
Sample Input for Custom Testing
pages = [5, 3, 4]days = 4
Sample Output
3

2. Code Question 2
Amazon games have introduced a new mathematical game for kids. You will be given nnn sticks and the player is required to form rectangles from those sticks.
Formally, given an array of nnn integers representing the lengths of the sticks, you are required to create rectangles using those sticks. Note that a particular stick can be used in at most one rectangle and in order to create a rectangle we must have exactly two pairs of sticks with the same lengths. For example, you can create a rectangle using sticks of lengths [2,2,5,5][2, 2, 5, 5][2,2,5,5] and [4,4,4,4][4, 4, 4, 4][4,4,4,4] but not with [3,3,5,8][3, 3, 5, 8][3,3,5,8]. The goal of the game is to maximize the total sum of areas of all the rectangles formed.
In order to make the game more interesting, we are allowed to reduce any integer by at most 1. Given the array sideLengths, representing the length of the sticks, find the maximum sum of areas of rectangles that can be formed such that each element of the array can be used as length or breadth of at most one rectangle and you are allowed to decrease any integer by at most 1. Since this number can be quite large, return the answer modulo 109+710^9 + 7109+7.
Note: It is not a requirement that all side lengths be used. Also, aaa modulo bbb here represents the remainder obtained when an integer aaa is divided by an integer bbb.
Example: The side lengths are given as sideLengths = [2, 6, 6, 2, 3, 5].
The lengths 2, 2, 6, and 6 can be used to form a rectangle of area 2×6=122 \times 6 = 122×6=12. No other rectangles can be formed with the remaining lengths. The answer is 12mod (109+7)=1212 \mod (10^9 + 7) = 1212mod(109+7)=12.
Function Description
Complete the function getMaxTotalArea in the editor below.
getMaxTotalArea has the following parameter(s):
int sideLengths[n]: the side lengths that can be used to form rectangles
Returns:
int: the maximum total area of the rectangles that can be formed, modulo 109+710^9 + 7109+7.
Constraints:
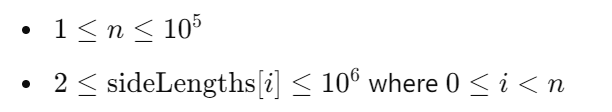
Sample Case 0
Sample Input for Custom Testing
sideLengths[] size n = 8sideLengths = [2, 3, 3, 4, 6, 8, 8, 6]
Sample Output
54
Explanation: Two rectangles can be formed. One has sides of 6 and 8, and the other by reducing 4 and one of the 3s by 1 has sides of 2 and 3. The total area of these rectangles is (6×8+2×3)mod (109+7)=54(6 \times 8 + 2 \times 3) \mod (10^9 + 7) = 54(6×8+2×3)mod(109+7)=54.
With our OA writing service, our Optiver company's OA perfectly achieved a full score. If you also need OA assistance, please contact us.
如果你需要OA代写,请联系我们, 确保满分。

