Welcome to our blog, where we reveal the solutions to two algorithm challenges from the JP Morgan Chase & Co. NAMR Software Engineer Program's campus hiring process. These tasks, designed to be completed in 60 minutes, test your skills in resource optimization and problem-solving.
We'll explore the Meeting Scheduler problem, which requires scheduling multiple meetings without conflicts, and the Reduction 3 problem, which involves reducing an array to a single element through strategic operations. Join us as we break down these challenges and provide clear, efficient solutions to help you ace your coding interviews!
Reduction 3
Given an array arr of nnn integers, a sequence of n−1 operations must be performed on the array.
In each operation:
- Remove the minimum and maximum elements from the current array and add their sum back to the array.
- The cost of an operation,
cost = ceil((minimum_element + maximum_element) / (maximum_element - minimum_element + 1))
Find the total cost to reduce the array to a single element.
Example: Given arr = [2, 3, 4, 5, 7]. The possible sequence of operations are:
- Choose 2 and 7, the cost = ceil((2 + 7) / (7 - 2 + 1)) = ceil(9 / 6) = 2. Remove 2 and 7, append 9,
arr = [3, 4, 5, 9], total_cost = 2. - Choose 3 and 9, the cost = ceil((3 + 9) / (9 - 3 + 1)) = ceil(12 / 7) = 2,
arr = [4, 5, 12], total_cost = 2 + 2 = 4. - Choose 4 and 12, the cost = ceil((4 + 12) / (12 - 4 + 1)) = ceil(16 / 9) = 2,
arr = [5, 16], total_cost = 4 + 2 = 6. - Choose 5 and 16, the cost = ceil((5 + 16) / (16 - 5 + 1)) = ceil(21 / 12) = 2,
arr = [21], total_cost = 6 + 2 = 8.
Return the total cost, 8.
Function Description: Complete the function findTotalCost in the editor below.
findTotalCost has the following parameter:
int arr[n]: the array to be reduced.
Returns:
int: the total cost to reduce the array to 1 element.
Constraints:
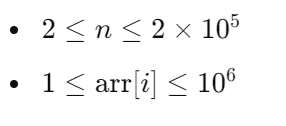
Sample Case 0
Sample Input for Custom Testing:
| STDIN | FUNCTION |
|---|---|
| 6 | arr[] size n=6 |
| 3 | arr = [3, 5, 2, 1, 9, 6] |
| 5 | |
| 2 | |
| 1 | |
| 9 | |
| 6 |
Sample Output: 10
Explanation: The possible sequence of operations are:
- Choose 1 and 9, the cost = ceil((1 + 9) / (9 - 1 + 1)) = ceil(10 / 9) = 2. Remove 1 and 9, append 10,
arr = [3, 5, 2, 6, 10], total_cost = 2. - Choose 2 and 10, the cost = ceil((2 + 10) / (10 - 2 + 1)) = ceil(12 / 9) = 2,
arr = [3, 5, 6, 12], total_cost = 2 + 2 = 4. - Choose 3 and 12, the cost = ceil((3 + 12) / (12 - 3 + 1)) = ceil(15 / 10) = 2,
arr = [5, 6, 15], total_cost = 4 + 2 = 6. - Choose 5 and 15, the cost = ceil((5 + 15) / (15 - 5 + 1)) = ceil(20 / 11) = 2,
arr = [6, 20], total_cost = 6 + 2 = 8. - Choose 6 and 20, the cost = ceil((6 + 20) / (20 - 6 + 1)) = ceil(26 / 15) = 2,
arr = [26], total_cost = 8 + 2 = 10.
Meeting Scheduler
On a given day, there are n meetings scheduled. There is a list of the meetings given as a 2D array, meetingTimings, of size n×mn \times mn×m, that contains the start and end times of the meetings. Determine the minimum number of meeting rooms needed to conduct all the meetings so that no meetings overlap in a meeting room.
Note: Meetings can end and begin at the same time in one room. For example, meetings at times [10, 15], and [15, 20] can be held in the same room.
Example: Suppose n=5, meetingTimings = [[1, 4], [1, 5], [5, 6], [6, 10], [7, 9]].
| Time | Event | Meetings Running |
|---|---|---|
| 1 | meetings 1 and 2 start | 1, 2 |
| 2 | 1, 2 | |
| 3 | 1, 2 | |
| 4 | meeting 1 ends | 2 |
| 5 | meeting 2 ends, meeting 3 starts | 3 |
| 6 | meeting 3 ends, meeting 4 starts | 4 |
| 7 | meeting 5 starts | 4, 5 |
| 8 | 4, 5 | |
| 9 | meeting 5 ends | 4 |
Compiled successfully. All available test cases passed.
Function Description: Complete the function getMinRooms in the editor below.
getMinRooms has the following parameter:
int meetingTimings[n][2]: the start and end times of the meetings.
Returns:
int: the minimum number of meeting rooms required.
Constraints:
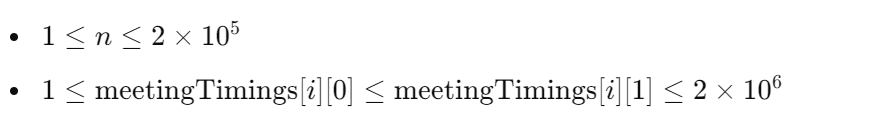
Sample Case 0
Sample Input for Custom Testing:
| STDIN | FUNCTION |
|---|---|
| 6 | meetingTimings[] size, n=6n = 6n=6 |
| 2 | constant integer, 2 |
| 2 8 | meetingTimings = [[2, 8], |
| 3 9 | [3, 9], |
| 5 11 | [5, 11], |
| 3 4 | [3, 4], |
| 11 15 | [11, 15], |
| 8 20 | [8, 20]] |
Sample Output: 3
Explanation: An optimal way to assign rooms for meetings is:
- Room 1: [2, 8], [8, 20]
- Room 2: [3, 4], [5, 11], [11, 15]
- Room 3: [3, 9]
经过我们的强力面试辅助,OA代写,候选人通过这些面试题的解析和沟通,面试官不仅了解了候选人的编程能力,也看到了我在解决问题过程中清晰的思路和有效的沟通技巧。这些不仅有助于应对 Meta 的面试,同时也能提升我们解决实际编程问题的能力。祝大家面试顺利!
如果你也需要我们的面试辅助服务,请立即联系我们。
With our powerful interview assistance and OA writing services, candidates can navigate these interview questions with ease. Through detailed analysis and effective communication, interviewers not only understand the candidate's programming skills but also see their clear problem-solving approach and strong communication abilities. This preparation not only helps in tackling interviews but also enhances our ability to solve real-world programming problems. Best of luck with your interviews!
If you need our interview assistance services, please contact us immediately.

