1. Code Question 1
Amazon's software team utilizes several algorithms to maintain data integrity, one of which targets the encoding of symmetrical names. Symmetrical names are unique in that they read identically in both directions, similar to palindromes in language parlance.
The chief aim of the algorithm is to rearrange the characters in the original symmetrical name according to these criteria:
- The rearranged name is a reshuffled version of the original symmetrical name.
- The restructured name should be symmetrical as well.
- This restructured name should be lexicographically smallest among all its symmetric permutations.
Given an initial symmetrical name that contains only lowercase English characters, compute the encoded name.
A string s is considered to be lexicographically smaller than the string t of the same length if the first character in s that differs from that in t is smaller. For example, "abcd" is lexicographically smaller than "abdc" but larger than "abad".
Note that the output encoded name could match the original name if it's already the smallest lexicographically.
Example The original string is nameString = "babab".
This can be reversed to give "abbba", which is a symmetric rearrangement of the original symmetrical name and is the smallest possible reverse order.
It satisfies all the requirements so return the string "abbba".
Returns
string: the encodednameString
Constraints
- 1≤∣nameString∣≤1051 \leq |nameString| \leq 10^51≤∣nameString∣≤105
nameStringconsists of lowercase English letters only.nameStringis a palindrome.
Input Format For Custom Testing
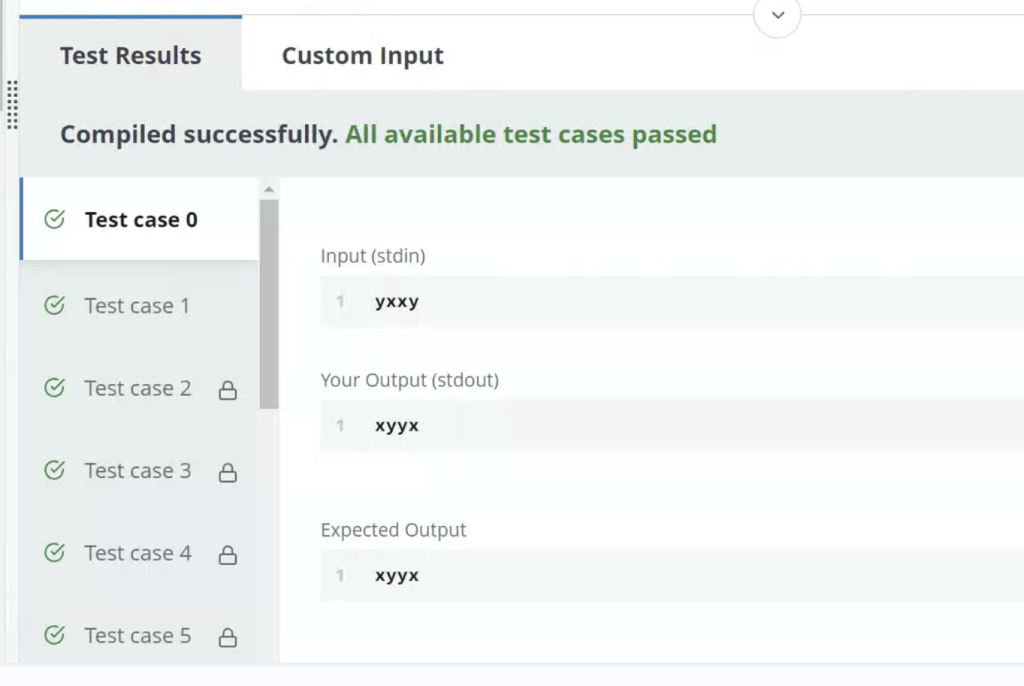
Sample Case 0
- Sample Input For Custom Testing
STDIN->FUNCTIONyxxy->nameString = "yxxy"
- Sample Output
xyyx
Explanation
Rearrange the original nameString to generate "xyyx", which is a palindrome and also the smallest possible reverse order.
Sample Case 1
- Sample Input For Custom Testing
STDIN->FUNCTIONded->nameString = "ded"
- Sample Output
ded
Explanation
The nameString already is the smallest possible reverse order in lexicographic terms.
2. Code Question 2
Amazon Web Services (AWS) stores grayscale images as an array of white and black pixels. The image is stored as a binary string where a white pixel is represented by ‘1’, and a black pixel is represented by ‘0’. The reverse of the image is represented as the reverse of this binary representation. For example, the reverse of "11010" is "01011". They want to store the reverse of each image as a backup. In order to reproduce the reverse from the original, the following operation can be performed any number of times: remove any character from the string and append it to the end of the string, i.e., choose any pixel and shift it to the end of the string.
Given the binary representation of pixels denoted by image, find the minimum number of operations needed to produce its reverse.
Example The pixel representation is image = "0100110".
The reverse of the image, i.e., the reverse of the string, is "0110010", and it can be produced using the following sequence of operations:
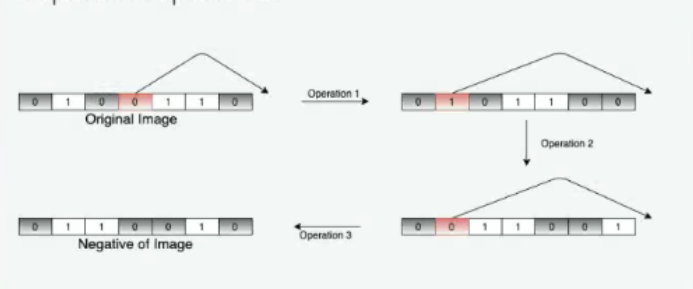
- Original image
0100110 - Operation 1
1001100 - Operation 2
0011001 - Operation 3
0110010
The string cannot be reversed in fewer than 3 operations. Return 3.
Function Description Complete the function findMinimumOperations in the editor below.
findMinimumOperations has the following parameter:
string image: a binary string that represents an image
Returns
int: the minimum number of operations required to produce a reverse, i.e., to reverse the string.
Constraints
- 1≤length of image≤1051 \leq \text{length of image} \leq 10^51≤length of image≤105
Input Format For Custom Testing The first line contains a string denoting image.
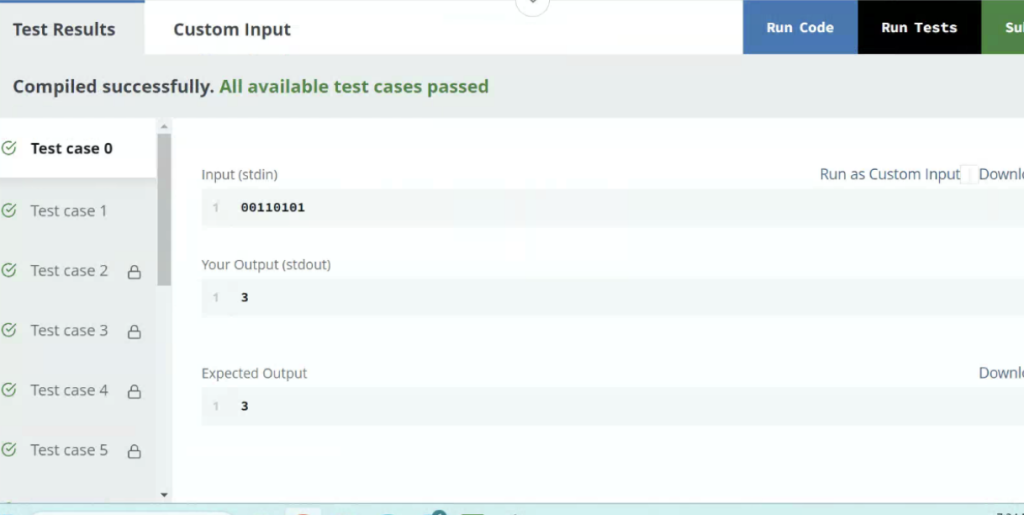
Sample Case 0
- Sample Input For Custom Testing
STDIN->FUNCTION00110101->image = "00110101"
- Sample Output
3
Explanation The string can be reversed in minimum 3 moves using the following sequence:
00110101->0010101100101011->0101011001010110->10101100
Sample Case 1
- Sample Input For Custom Testing
STDIN->FUNCTION101011->image = "101011"
- Sample Output
2
Explanation The string can be reversed as follows:
101011->110110110110->110101
如果您也有OA代写的需求,请联系我们,我们服务至上,励志做北美面试支持机构第一品牌。 CSOAHELP
