Amazon NG 岗位火热开放中，目前 OA的组合是90分钟的2道coding和system design的选择题，今天我们一起来看看其中的2道coding题目吧。

Code Question 1

Amazon's AWS provides fast and efficient server solutions. The developers want to stress-test the quality of the servers' channels. They must ensure the following:

• Each of the packets must be sent via a single channel.
• Each of the channels must transfer at least one packet.

The quality of the transfer for a channel is defined by the median of the sizes of all the data packets sent through that channel.

Note: The median of an array is the middle element if the array is sorted in non-decreasing order. If the number of elements in the array is even, the median is the average of the two middle elements.

Find the maximum possible sum of the qualities of all channels. If the answer is a floating-point value, round it to the next higher integer.

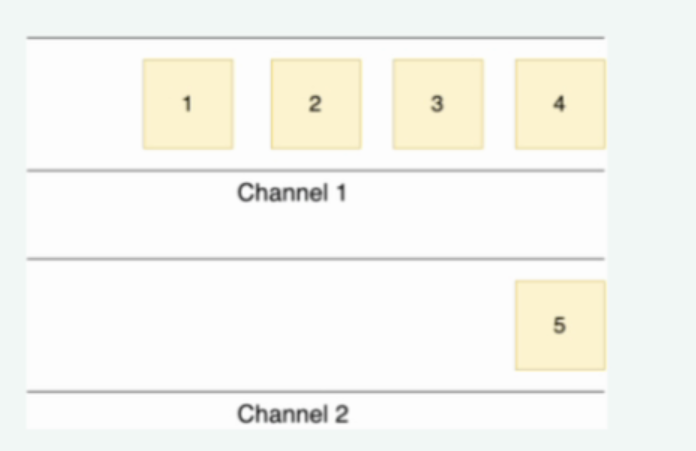
Example

At least one packet has to go through each of the 2 channels. One maximal solution is to transfer packets {1, 2, 3, 4} through channel 1 and packet {5} through channel 2.

---

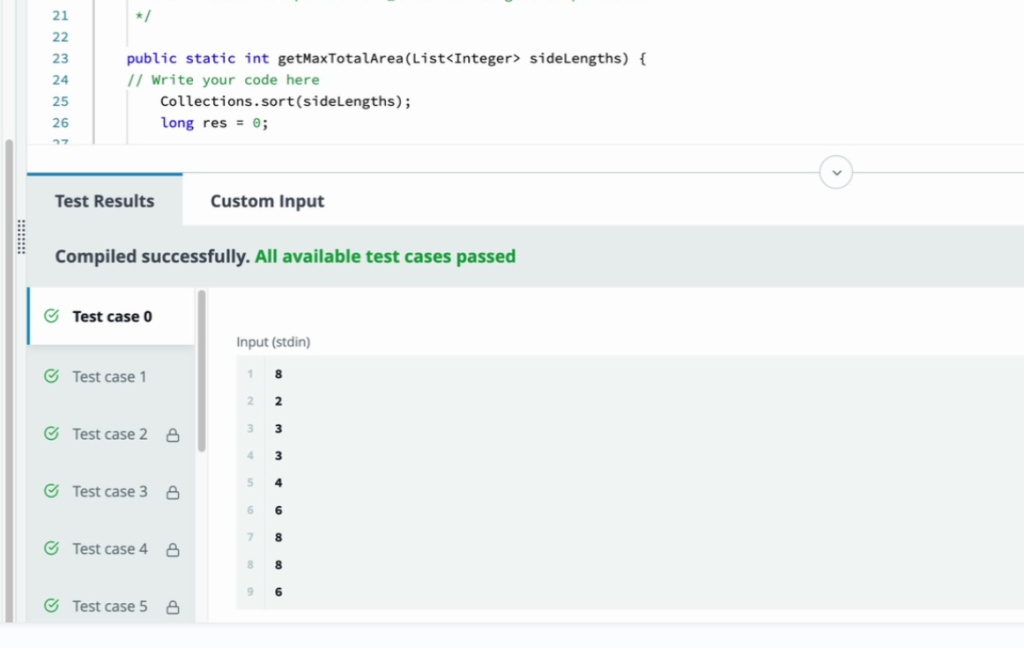
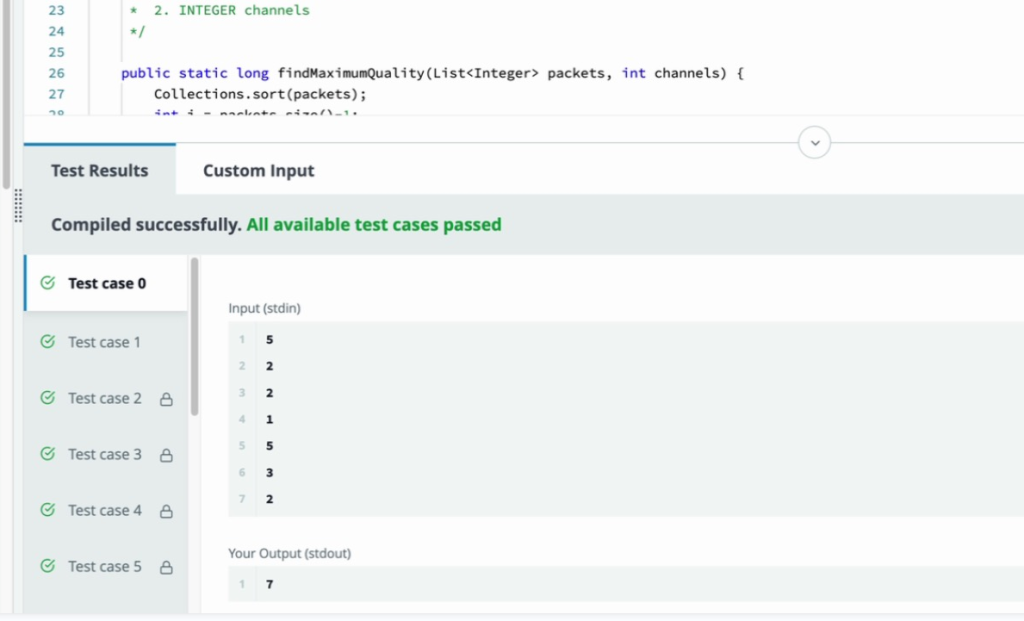
Code Question 2

Amazon games have introduced a new mathematical game for kids. You will be given nnn sticks and the player is required to form rectangles from those sticks.

Formally, given an array of nnn integers representing the lengths of the sticks, you are required to create rectangles using those sticks. Note that a particular stick can be used in at most one rectangle and in order to create a rectangle we must have exactly two pairs of sticks with the same lengths. For example, you can create a rectangle using sticks of lengths [2,2,5,5][2, 2, 5, 5][2,2,5,5] and [4,4,4,4][4, 4, 4, 4][4,4,4,4] but not with [3,3,5,8][3, 3, 5, 8][3,3,5,8]. The goal of the game is to maximize the total sum of areas of all the rectangles formed.

In order to make the game more interesting, we are allowed to reduce any integer by at most 1. Given the array sideLengths, representing the lengths of the sticks, find the maximum sum of areas of rectangles that can be formed such that each element of the array can be used as length or breadth of at most one rectangle and you are allowed to decrease any integer by at most 1. Since this number can be quite large, return the answer modulo 109+710^9 + 7109+7.

Note: It is not a requirement that all side lengths be used. Also, a modulo bbb here represents the remainder obtained when an integer aaa is divided by an integer bbb.

Example

The lengths 2, 2, 6, and 6 can be used to form a rectangle of area 2×6=122 \times 6 = 122×6=12. No other rectangles can be formed with the remaining lengths. The answer is 12mod  (109+7)=1212 \mod (10^9 + 7) = 1212mod(109+7)=12.

Function Description

Complete the function getMaxTotalArea in the editor below. getMaxTotalArea has the following parameter(s):

• int sideLengths[n]: the side lengths that can be used to form rectangles

Returns

• int: the maximum total area of the rectangles that can be formed, modulo 109+710^9 + 7109+7.

Constraints

• 1≤n≤1051 \leq n \leq 10^51≤n≤105
• 2≤sideLengths[i]≤1062 \leq \text{sideLengths}[i] \leq 10^62≤sideLengths[i]≤106 where 0≤i<n0 \leq i < n0≤i<n

Input Format For Custom Testing

Sample Case 0

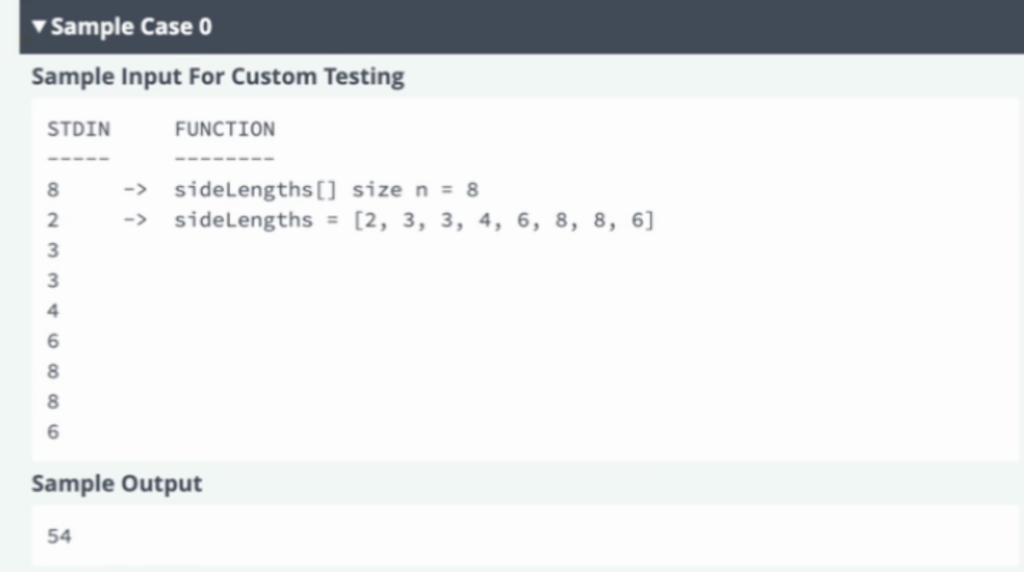
Explanation Two rectangles can be formed. One has sides of 6 and 8, and the other by reducing 4 and one of the 3s by 1 has sides of 2 and 3. The total area of these rectangles is (6×8+2×3)mod  (109+7)=54(6 \times 8 + 2 \times 3) \mod (10^9 + 7) = 54(6×8+2×3)mod(109+7)=54.

这两道题目设计合理，难度适中偏难，如果您对自己完成这2题没有信心，可以联系我们，我们将确保您的算法题获得满分。同时我们还提供面试代面，面试辅助等服务。详情请查看

We successfully tackled these two questions in just over ten minutes. If you require assistance with completing Online Assessments (OA), please do not hesitate to contact us. Additionally, we offer services such as interview proxying and interview coaching. Our goal is to provide you with comprehensive support to ensure you excel in your career endeavors.