Ubiquity Technology 春招笔试开始,知名外企Ubiquity开启了180分钟的地狱笔试模式。我们一起来看看其中之一的这个魔方的算法问题吧。

已知奇数阶魔方矩阵是指这样的二维矩阵,它的行数和列数为相等的奇数N,把1~N^2连续的整数填入到 N^2个格子中,它的每一行、每一列和对角线之和均相等。对于任何一个奇数阶魔方矩阵都存在如下通用解法:
一个奇数阶魔方矩阵 Array[N][N],(下标从0到 N-1)
- 第 0 行中间一列开始填入整数 1,即 Array[0][(N - 1) / 2] = 1;
- 如果当前填入数字的位置为第 0 行最后一列(矩阵右上角的 Array[0][N-1]),下一个填入的位置是行数加一,列不变(Array[1][N-1]);
- 如果当前填入行数为第 0 行但不是最后一列,那么下一个数字填入的行数为最后一行,列数为当前数字所在列的下一列(Array[N-1][col+1]);
- 如果当前填入行数不是第0行,但已经是最后一列,那么下一个数字填入的行数为当前数字的上一行第0列(Array[row-1][0]);
- 如果条件1、2、3、4都不满足,下一个数字填入的行数为当前行的上一行,列数为当前列的下一列;(行数递减,减到第0行则回到最后一行;列数递增,增到最后一列则回到第 0 列)
- 如果不满足条件1、2、3、4但是按照条件5计算出的位置已经填写过数字了,那么下一个填入的位置为当前填入位置行数加一,列不变(Array[row+1][col]);
- 按照1~6的规则依次填入1~N^2这些整数,最终得到的就是奇数阶魔方矩阵的一个通用解。
比如3阶魔方矩阵的每行、每列和每个对角线数字之和都是15;
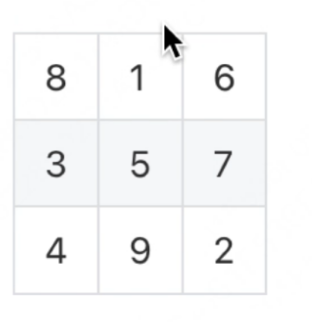
5阶魔方矩阵的每行、每列和每个对角线数字之和都是65;

请按照上述奇数阶魔方矩阵的通用解描述实现对应的代码。要求程序输入参数为一个正整数奇数(9,11,15等),输出为矩阵的行序遍历输出(每个数组元素单独一行)。
(注意事项:魔方矩阵有多种解,不同解的矩阵元素排布存在差异,请严格按照规则实现)
我们一起来看看思路
奇数阶魔方矩阵是一种每一行、每一列及两个对角线上的数相加都相等的方阵。对于 𝑁N 阶的魔方矩阵(其中 𝑁N 是边长上的单元数,且 𝑁N 是奇数),可以通过下列步骤来填充矩阵:
- 从第 0 行的中间列开始,填入数字 1,即
Array[0][(N-1)/2] = 1。 - 如果当前填入数字的位置是第 0 行最后一列(即矩阵的右上角,
Array[0][N-1]),则下一个填入的位置是行数加一,列数不变(Array[1][N-1])。 - 如果当前填入的行数是第 0 行但不是最后一列,那么下一个数字填入的位置是最后一行,列数为当前数字所在列的下一列(
Array[N-1][col+1])。 - 如果当前填入的行数不是第 0 行,但已经是最后一列,那么下一个数字填入的位置是当前数字的上一行第 0 列(
Array[row-1][0])。 - 如果以上条件都不满足,那么下一个数字填入的位置是当前行的上一行,列数为当前列的下一列。如果行数减到 0,则回到最后一行;如果列数增加到最后一列,则回到第 0 列。
- 如果不满足规则 1,2,3,4 但按照规则 5 计算出的位置已经被填入过数字,那么下一个填入的位置是当前位置的行数加一,列数不变(
Array[row+1][col])。 - 按照上述规则,依次填入 11 到 𝑁2N2 的整数,最终得到的矩阵就是一个奇数阶魔方矩阵的解。
我们提供OA代做服务,请注意,如果你是在OA的过程中搜索到本文,那么不幸的是我们将无法为您服务。得益于我们优质的服务和有竞争力的价格,我们的OA代做服务必须要预约才能够实行。我们的OA代做是一项收费服务,如果是希望免费获得答案的人不要联系我们。
We provide OA agency services. Please note that if you search for this article during the OA process, unfortunately, we will not be able to serve you. Thanks to our high-quality service and competitive pricing, our OA outsourcing service requires an appointment to be implemented. Our OA agency is a paid service. If you want to get answers for free, please do not contact us.
联系我,查看题目全文。OA代做,代面试,面试代面,面试辅助。联系我 我们公开透明报价,做华人社区面试suport第一品牌。
