snowflake OA 以超高难度闻名于北美CS圈。但是在我们的代做老师的操作下,完全不是问题。轻松AC三道题。我们可以使用任意客户指定的语言,话说对于我们这种专业选手来说,语言和技术栈完全不是问题的。
Q1.calculateMax
network_nodes = 4, network_from = [1, 2, 3], network_to = [2, 3, 4], and frequency = [1, 3, 2, 1]
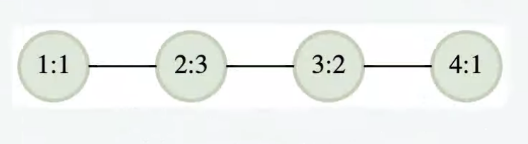
The graph is labeled device:frequency. Check if a message can be passed for each pair of devices and distance.
- (1,2):(1,2): The difference between frequencies, 1 and 3, is greater than 1. A message cannot be transmitted.
- (1,3):(1,3): A message cannot be transmitted due to failure at (1,2)(1,2).
- (1,4):(1,4): A message cannot be transmitted due to failure at (1,2)(1,2).
- (2,3):(2,3): The difference in frequencies, 3 and 2, is 1. A message can be transmitted.
- (2,4):(2,4): Differences are such that a message can be transmitted from 2->3 and 3->4. The distance is 2.
- (3,4):(3,4): A message can be transmitted, and the distance is 1.
The longest path, and the answer, is 2.
Function Description
Complete the function calculateMax in the editor below.
calculateMax has the following parameters:
Q2.Coloring Houses
The city of Hackerland can be represented with an even number n houses arranged in a row. A painter must paint the houses using at most three colors. The following conditions must hold true:
- No two adjacent houses are the same color.
- The houses which are at the same distance from both ends must not be colored with the same color. For example, n=6 then houses will be [1,2,3,4,5,6], so the houses at the same distance from both the ends will be [1,6], [2,5], [3,4].
The task is to find the number of ways to paint the houses using at most three colors such that both the above conditions hold true. Since the answer can be large, report it modulo 109+7109+7. Two ways are considered different if at least one house is colored differently.
Example
For n = 4, some of the possible valid arrangements are:
- (𝑐𝑜𝑙𝑜𝑟1,𝑐𝑜𝑙𝑜𝑟2,𝑐𝑜𝑙𝑜𝑟3,𝑐𝑜𝑙𝑜𝑟2)(color1,color2,color3,color2)
- (𝑐𝑜𝑙𝑜𝑟1,𝑐𝑜𝑙𝑜𝑟3,𝑐𝑜𝑙𝑜𝑟1,𝑐𝑜𝑙𝑜𝑟3)(color1,color3,color1,color3)
The number of ways to paint 4 houses using three colors is 18. Return 18 modulo (109+7)(109+7) which is 18.
Q3.Minimum Segments
Given is an array consisting of n intervals. The ith interval is of type (a[i], b[i]). Also given is an integer k. Add exactly one segment (a, b) to the array such that b - a ≤ k and the modified array can be separated into the minimum number of connected sets.
A set of segments (a[1], b[1]), (a[2], b[2]), ..., (a[n], b[n]) is connected if every point in the segment (min(a[1], a[2], ..., a[n]), max(b[1], b[2], ..., b[n])) is covered by some segment (a[i], b[i]) in the set.
联系我,查看题目全文。OA代做,面试代面,面试辅助。联系我 我们公开透明报价,做华人社区面试suport第一品牌。

