1. Heap Operations Complexity
A heap is a special type of binary tree in which every parent node is less than or equal to its child node(s) (min-heap) or greater than or equal to its child node(s) (max-heap). This property must be recursively true for all sub-trees in that binary tree.
Given the following Heap class:

The task is to correctly implement the insert(element) and removeTop() methods considering they should run in O(logn) and O(1) time complexities respectively.
insert(element)method: adds a new element to the heap, maintaining the heap property, which requires the operation 'siftUp', where the added element is moved up the heap until the heap property is restored.removeTop()method: removes the top-most element, and to restore the heap property, it employs 'siftDown', moving down the heap accordingly.
Which of the following code snippets achieves this?
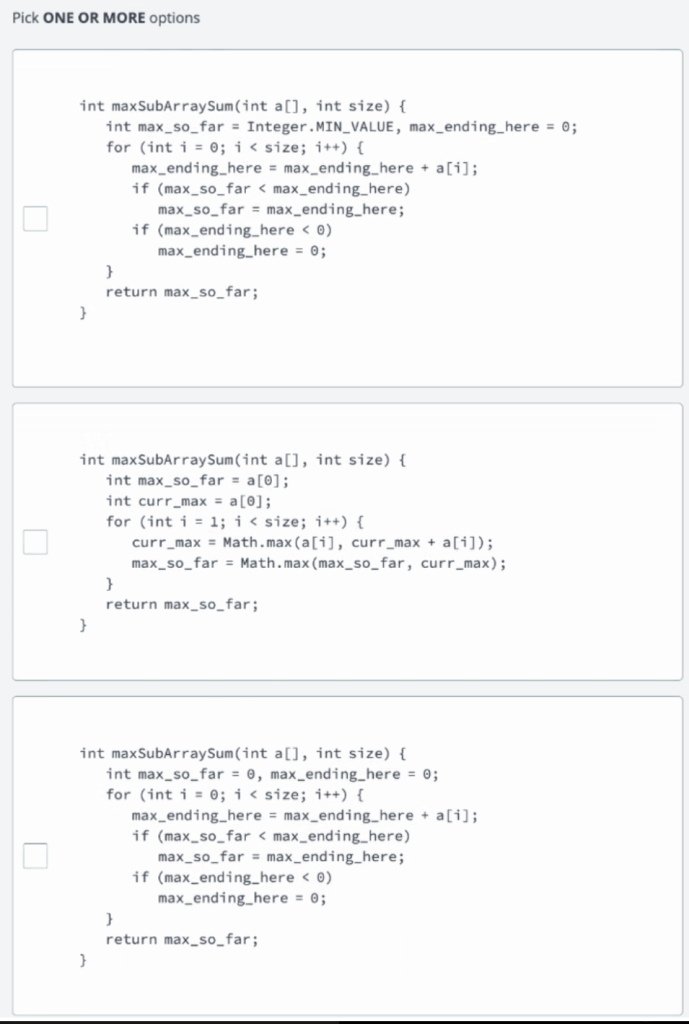
2. Maximum Subarray Sum
Which two pseudo-code snippets implement Kadane's algorithm to find the maximum subarray sum?
4. Longest Concave Subsequence
A concave subsequence is a subsequence where the first an last elements are greater than all other elements in between. For example, [100, 0, 25, 11, 200] is concave, while [100, 0, 110, 200] is not since the third element is greater than the first element.
Given an array that contains a permutation of n integers, arr[n], determine length of the longest concave subsequence.
A permutation is a sequence of integers from 1 to n that contains each number exactly once. For example [1, 3, 2] is a permutation while [1, 2, 1] and [1, 2, 4] are not.
A subsequence is derived from a sequence by deleting zero or more elements without changing the order of the remaining elements. For example [3, 4] is a subsequence of [5, 3, 2, 4], but [4, 3] is not.
If you're afraid that you can't solve the OA on your own, please scan the code to contact me or telegram

