Twilio公司加拿大岗位的OA最近发放中，由3个算法题和6个选择题构成。The OA for Canadian positions at Twilio has recently been released, consisting of 3 algorithm questions and 6 multiple choice questions.

1. Array Representations

Objective: Find the minimum k for which an integer can be expressed as a sum of k integers that meet the following criteria:

• Each integer is greater than 0.
• Exactly (k - 1) integers are even powers of 2.
• One integer is less than 4.

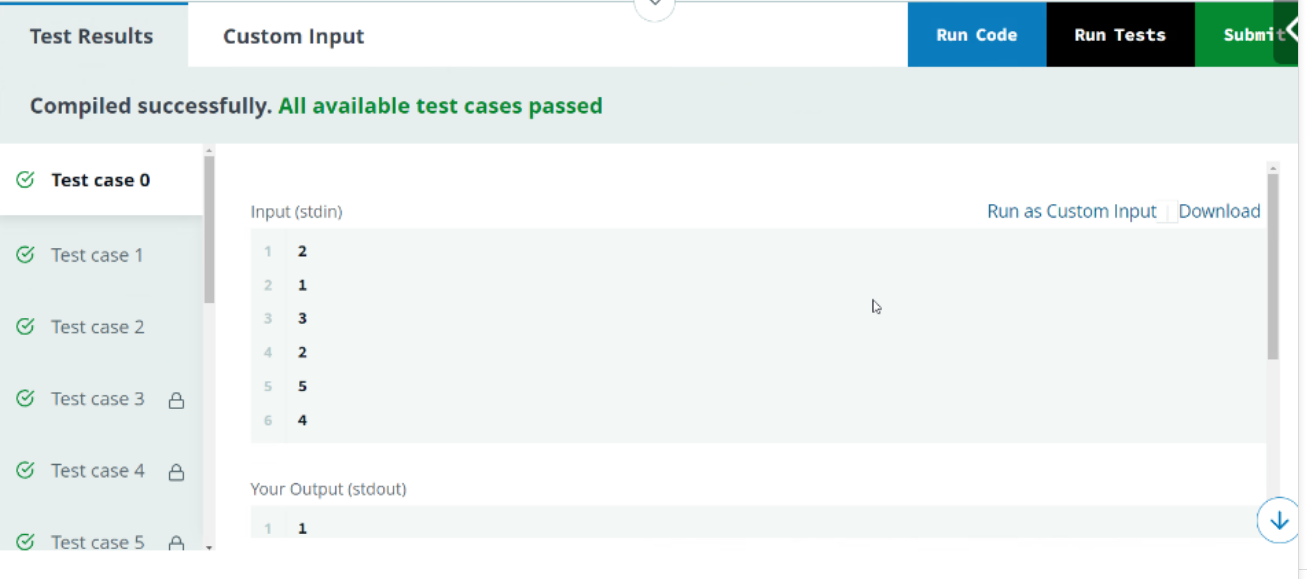
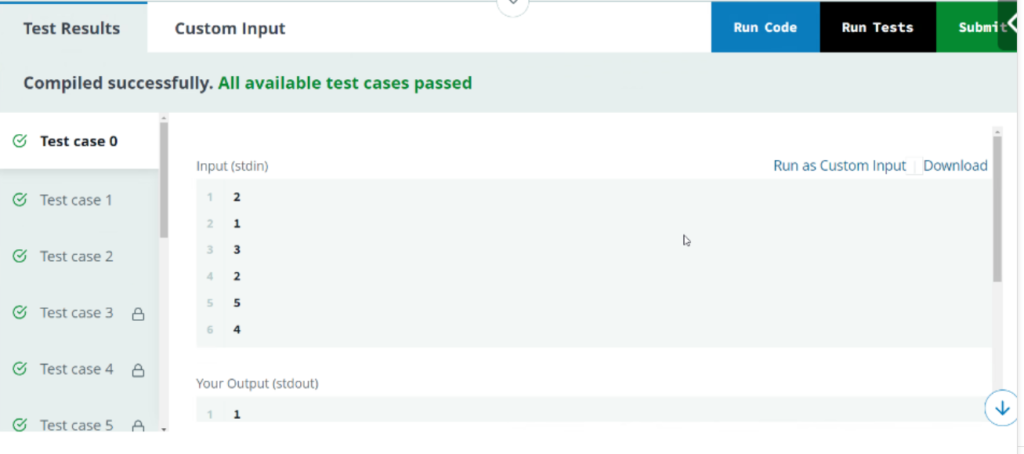
Example: For an array arr = [5, 1, 4, 6, 10], the output should be [2, 1, -1, 2, 3].

Function:

pythonCopy code

def getMinimumKValues(arr): # Your code here

Parameters:

• int[] arr: An array of integers.

Returns:

• int[]: An array where the ith element is the minimum k value for the ith element in arr or -1 if it cannot be expressed as required.

Constraints:

• 1 ≤ n ≤ 2 * 10^5
• 1 ≤ arr[i] ≤ 2^30

Examples and Explanations:

• 5 can be expressed as 1 + 4, so k = 2.
• 1 can be expressed as 1, so k = 1.
• 4 cannot be expressed under the given conditions, so the answer is -1.
• 6 can be expressed as 2 + 4, so k = 2.
• 10 can be expressed as 2 + 4 + 4, so k = 3.

第二题非常的取巧，有效利用树数据的特性的话，可以只需要一行就解决这道题。The second question is very tricky. If you effectively use the characteristics of tree data, you can solve this question with only one line.

2.Customizable Tours with GoWorld

Problem Statement: GoWorld, a travel agency, provides customizable tours where travelers can select their preferred tourist spots. Each spot is connected by roads (edges), forming a tree-like structure. The objective is to compute the minimum cost to travel from a start node to an end node, covering all nodes at least once.

Example: Given a tree with nodes labeled from 1 to 4, starting at node 1 and ending at node 4, find the minimum cost path.

Function Description: Write a function findMinimumCost to compute the minimum cost path.

pythonCopy code

def findMinimumCost(tree_nodes, tree_from, tree_to, tree_weight, start, end): # Your code here

Parameters:

• tree_nodes: The number of nodes in the tree.
• tree_from, tree_to, tree_weight: Three integer arrays where tree_from[i] and tree_to[i] denote the nodes connected by the ith edge, and tree_weight[i] denotes the weight of the ith edge.
• start: The start node of the path.
• end: The end node of the path.

Returns:

• An integer representing the minimum cost path value.

Constraints:

• 1 ≤ tree_nodes ≤ 10^5
• 1 ≤ tree_from[i], tree_to[i], start, end ≤ tree_nodes
• 1 ≤ tree_weight[i] ≤ 10^4

Since a tree is a graph with no cycles, there is exactly one path between any two nodes. Therefore, the minimum cost path from any start to any end node, which visits all nodes at least once, will necessarily involve traversing each edge once. This is why the sum of the weights of all the edges, sum(tree_weight), suffices to find the solution.

This problem examines the understanding of the tree data structure, specifically the properties of trees and how they are traversed. Due to the non-cyclical nature of trees and the fact that there is a unique simple path between any two nodes in a tree, the minimum cost path that traverses all nodes is simply the sum of the weights of all the edges. This represents a simplification of tree traversal algorithms, which would typically require more complex solutions, but due to the unique characteristics of trees, this problem has a very concise solution.

3-8是选择题，如果有需要可以联系我。3-8 are multiple choice questions, please contact me if necessary.

9.Segment Intersections

Objective: Given a list of segments on a number line, find the number of intersections for each segment with all other segments.

The "Segment Intersections" coding problem is an interesting and challenging algorithmic puzzle that involves understanding and manipulating intervals

接受预约中，包AC

我们可以在线协助您通过任何的OA，不管是开摄像头还是任何作弊检测方案我们都能够绕过

Accepting bookings, ensure AC.

We can assist you online with any online assessment, and we can bypass any cheating detection mechanisms, including those that require the use of a camera

contact me to slove OA （Paid ）

telegram