一阵寒暄后,面试官抛出了这道题
Implement the function pow(x, n), which calculates x^n.
Note that you cannot use any existing functions that implement pow, as that would trivialize the problem.
Example 1: Input: x = 2, n = 5 output = 32
面对这个面试题,我会首先确认问题的边界条件,例如n的正负或者特殊值处理,以及x的类型和范围。然后,我会简要介绍我的解题思路,包括暴力解法和优化方法。对于x^n,最直观的方法是将x乘以自身n次,但这种方法的时间复杂度是O(n),在n非常大时效率低下。
When presented with the interview question of implementing a pow(x, n) function, which calculates x to the power of n, my first step would be to clarify the problem's constraints and edge cases. This includes inquiring about the range and type of x, as well as handling scenarios where n is negative or zero.
我接着会提到一种更高效的方法——快速幂算法。快速幂算法的核心思想是分治,将x^n分解为若干个小的部分,利用n的二进制表示来降低计算的复杂度。具体来说,我们可以将n表示为二进制数,并利用x^n = x^(2^k) * x^(2^(k-1)) * ... * x^(2^0)的性质,其中k是n的位数。这样,我们只需要对n的每一个二进制位进行检查,如果该位为1,则将当前的x^(2^i)(i为该位的位置)乘到结果上。这种方法将时间复杂度降低到了O(log n)。
I would start by outlining my approach to the interviewer, beginning with a brute-force method and then introducing a more efficient solution. The straightforward method involves multiplying x by itself n times, but this approach has a time complexity of O(n), which can be impractical for large values of n.
Next, I would discuss a more sophisticated method known as the fast exponentiation algorithm. The essence of this algorithm is a divide-and-conquer strategy that breaks down the computation of x^n into smaller chunks, taking advantage of the binary representation of n to reduce computational complexity. Specifically, it leverages the fact that x^n = x^(2^k) * x^(2^(k-1)) * ... * x^(2^0), where k is the number of bits in n. This means we only need to consider each bit of n, multiplying the result by x^(2^i) (where i is the position of the bit) if that bit is set to 1. This algorithm reduces the time complexity to O(log n).
以下是我的伪代码实现:
Here's the pseudocode for this solution:
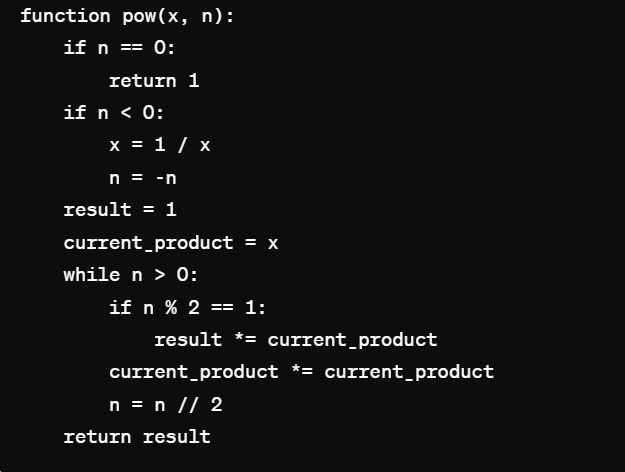
在解释这个伪代码时,我会强调几个关键点:
- 处理
n为负数的情况,这时候我们需要计算1/x的-n次幂。 - 初始化结果
result为1,因为任何数的0次幂都是1。 - 使用
current_product变量跟踪x的幂次方的值,这个值在每次循环时平方,以此实现快速幂。 - 通过
n的二进制表示来决定是否将current_product乘到result上。 - 通过
n = n // 2来实现对n的二进制位的遍历。
通过这种方式,我能够高效地解决这个问题,并且能够清晰地向面试官展示我的思路和代码实现能力。
While explaining this pseudocode, I would emphasize several key points:
- Handling negative
nby computing the power of1/xto the-n. - Initializing
resultto 1 because any number to the power of 0 is 1. - The use of a
current_productvariable to keep track of the power ofx, which is squared in each iteration to achieve fast exponentiation. - Deciding to multiply
current_productwithresultbased on the binary representation ofn. - Iterating through the bits of
nby dividingnby 2 in each step.
This approach not only allows me to efficiently solve the problem but also demonstrates clear thinking and code implementation skills to the interviewer.
根据需要我们可以提供面试辅助,代面试 等特殊服务,帮您拿到offer
求职上岸绝不是一朝一夕之功,低年级同学想要拥有一份大厂实习经历,需要大家提前做好充足的准备。
【Go】了解求职服务,全面提升求职竞争力!
We can provide special services such as interview assistance and proxy interviews as needed to help you secure your offer
Finding a job is not something that can be achieved overnight. If younger students want to have an internship experience in a large company, they need to make sufficient preparations in advance.
【 Go 】 Learn about job search services and comprehensively enhance your job search competitiveness!

