📌 Problem: Linear Interpolator

You are asked to implement a linear interpolator. Namely you are given n points on a 2-dimensional coordinate system (known as the knot points).

When these points are sorted by their x coordinates and then connected together using straight lines (in their sorting order), they define a piecewise-linear function L(x) known as the linear interpolation.

When x is outside the range of all knot points, L(x) is defined by extrapolation, i.e., extending the straight line connecting its two nearest knot points.

🧠 Function Signature

def linear_interpolate(
    n: int,
    x_knots: List[float],
    y_knots: List[float],
    x_input: float
) -> float

• n: number of knot points
• x_knots: list of x-coordinates of the knot points
• y_knots: list of y-coordinates of the knot points
• x_input: the query x-value

Return the value of the interpolated function L(x_input).

🧾 Behavior Rules

• If multiple knot points share the same x-coordinate:
  • When x_input <= x, use the smallest y among those points.
  • When x_input > x, use the largest y among those points.
• For extrapolation:
  • If x_input < min(x_knots), use the two smallest x values.
  • If x_input > max(x_knots), use the two largest x values.
  • Follow the same tie-breaking rule as above.

📌 Constraints

• 1 < n <= 100,000
• x_knots and y_knots are guaranteed to have the same length
• x_knots and y_knots are not sorted
• You must implement interpolation by hand; do not use any interpolation libraries
• All floats are multiples of 0.001 (equality comparison is unambiguous)

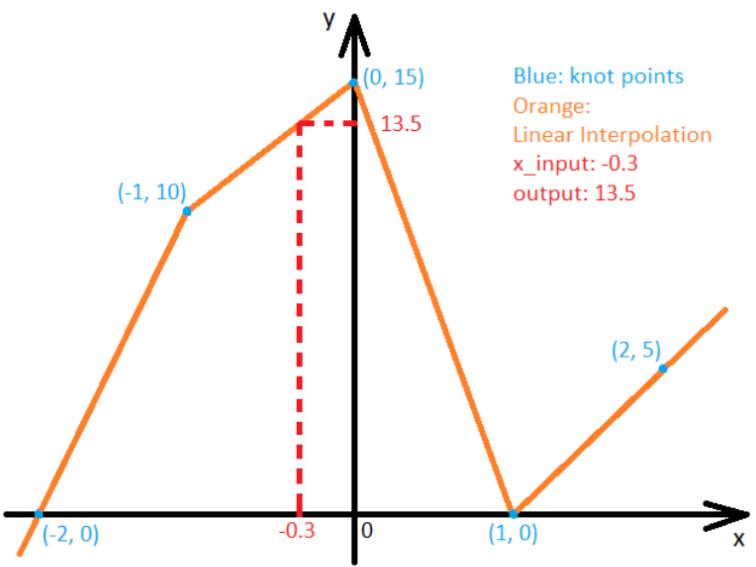
📥 Sample Input

n = 5
x_knots = [-2.0, -1.0, 0.0, 1.0, 2.0]
y_knots = [0.0, 10.0, 15.0, 0.0, 5.0]
x_input = -0.3

📤 Sample Output

13.5

📈 Explanation

x_input = -0.3 lies between -1.0 and 0.0.
The interpolation is performed on the line segment from (-1.0, 10.0) to (0.0, 15.0) using the linear formula:$$L(x) = y_1 + (x - x_1) \cdot \frac{y_2 - y_1}{x_2 - x_1}$$

So,$$L(-0.3) = 10.0 + (-0.3 + 1.0) \cdot \frac{15.0 - 10.0}{0.0 + 1.0} = 13.5$$

Efficient Regression V5

Part One

Implement a function to compute univariate OLS regression coefficients (betas) between pairs of asset returns from two dataframes dfx and dfy, where each column xi in dfx corresponds to column yi in dfy.

Regression form:$$y_i = \beta_i \cdot x_i$$yi​=βi​⋅xi​

No intercept should be fitted.

def compute_betas(dfx: pd.DataFrame, dfy: pd.DataFrame) -> List[float]

• dfx: dataframe with predictor values x0 to xN
• dfy: dataframe with target values y0 to yN
• Returns: list of N float values for each beta.

Part Two

Now compute online (cumulative) betas using a list of batches dfxs and dfys, each being a list of dataframes.

For each batch index j, compute betas using cumulative data from batch 0 to j.

def compute_betas_online(
    dfxs: List[pd.DataFrame],
    dfys: List[pd.DataFrame]
) -> List[List[float]]

• dfxs, dfys: lists of DataFrames with aligned shapes
• Returns: list of lists of float — betas for each cumulative batch.

Daily Temperature By Town

You are given daily temperature readings for multiple towns and NYC.

Part One:

Answer these questions:

1. Town with highest temperature standard deviation
2. Median NYC temperature on days when Town2 ∈ [90, 100]
3. Sum of absolute regression coefficients from town to NYC (using simple linear regression without intercept)
4. Town most predictive of NYC (min MSE with intercept)
5. Two towns most predictive jointly of NYC (min MSE with intercept)

def q1_q5(df: pd.DataFrame) -> List

Part Two:

Find 5 towns most predictive of NYC (lowest MSE with intercept, using greedy selection).

def q6(df: pd.DataFrame) -> List

• You must implement a greedy approximation, exhaustive search will time out.

我们长期稳定承接各大科技公司如Visa、TikTok、Google、Amazon等的OA笔试代写服务，确保满分通过。如有需求，请随时联系我们。

We consistently provide professional online assessment services for major tech companies like TikTok, Google, and Amazon, guaranteeing perfect scores. Feel free to contact us if you're interested.