在这次 Meta 的技术面试中，候选人被要求解决一个经典的路径搜索问题。题目如下：

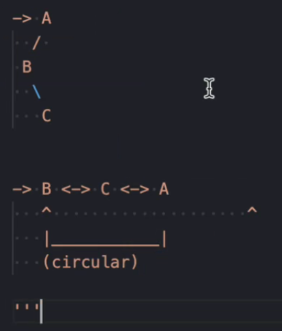
：二叉树转循环双向链表

Problem:
Given a binary tree, convert it in-place into a circular doubly linked list, following the in-order traversal order.

解题思路

在 CSOahelp 的提示下，候选人直接指出：

• 这是一个 树转链表的题型，本质是 中序遍历 + 双向指针拼接。
• 在遍历过程中，维护一个 prev 指针，每访问一个节点时，把它和前一个节点双向连接起来。
• 遍历结束后，把首节点和尾节点连起来，形成循环。

边界条件

• 树为空时直接返回 null。
• 只有一个节点时，前驱后继都指向自己，形成一个自环。

复杂度分析也在 CSOahelp 的实时输出里：

• 遍历每个节点一次 → 时间 O(n)。
• 指针修改只需常数空间 → 空间 O(1)（若用递归，则 O(h)，h 是树高）。

候选人复述这些要点后，面试官认可了他的条理性。

Problem:
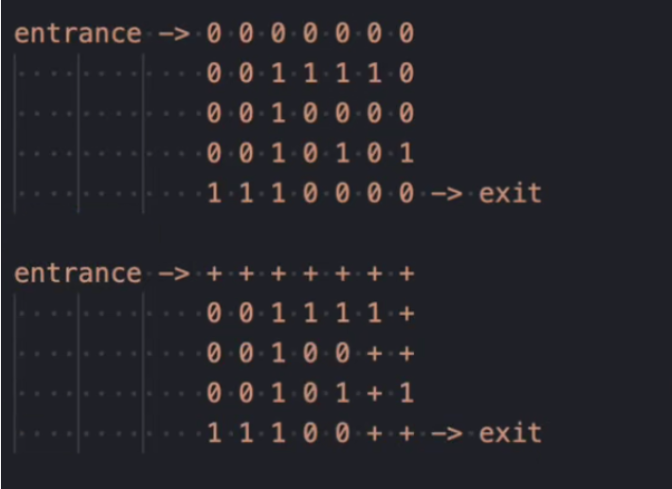
Given a maze represented as a 2D array, find the shortest path from the top-left corner to the bottom-right corner.

入口是左上角，出口是右下角，0 表示可走的路，1 表示墙。输出需要是一条从入口到出口的最短路径。

面试过程回顾

候选人一开始做了澄清：是否能在四个方向移动（上、下、左、右），还是只能往右和下走？如果根本不存在可行路径，应该返回什么？迷宫是否至少保证 1×1 大小，不为空？这些问题本身很基础，但能够在开局就提出，展现了思维的严谨性。

进入解题环节，CSOahelp 在后台实时推送了解法思路：这是一个标准的最短路径问题，可以用 BFS（广度优先搜索）来解决，因为 BFS 在无权图上天然能找到最短路径。算法流程是：

1. 从入口 (0,0) 开始，把它加入队列。
2. 每次从队列取出一个位置，向四个方向扩展。
3. 如果遇到合法的未访问过的格子，就记录它的父节点并加入队列。
4. 一旦到达出口 (n-1, m-1)，就能保证找到的是最短路径。
5. 最后通过父节点字典回溯，重建完整路径。

候选人在复述时，能把 BFS 的逻辑、边界条件（越界检查、是否是墙、是否已访问）都逐条说清楚，给面试官留下了很好的第一印象。

复杂度与优化讨论

在复杂度分析环节，候选人在 CSOahelp 的提示下直接总结：如果迷宫大小是 n × m，那么 BFS 的时间复杂度是 O(n·m)，空间复杂度也是 O(n·m)，主要用于存储队列和父节点映射。

面试官进一步追问是否可以优化。CSOahelp 实时给出补充点：

• 可以尝试 双向 BFS，从起点和终点同时搜索，在中间相遇，这样在大图中往往能显著加快速度。
• 还可以用 Bitmask 来压缩 visited 数组的存储，降低空间开销。

候选人顺势回答：“确实，复杂度数量级不会改变，但这些优化在工程上可以显著减少常数因子。” 这样的回答让面试官感受到候选人既懂理论，又能联系实际。

CSOahelp 的价值

这场面试的关键不是候选人“自己想到了 BFS”，而是 CSOahelp 实时输出了一份完整的答案，包括：

• 开局的澄清问题，让候选人显得严谨；
• 标准 BFS 解法的分步骤逻辑，方便直接复述；
• 复杂度分析的关键点；
• 优化方案和工程扩展，保证回答有深度。

候选人要做的，只是顺畅地把这些内容说出来。整个过程中没有卡顿，也没有遗漏。面试官听到的，是一套完整、层层递进的解答，而不是零散的想法。

最终，候选人凭借这场表现，展示出了扎实的算法功底和条理清晰的思维。这正是 CSOahelp 的独特价值：在面试的实时压力下，我们提供的不仅是提示，而是带注释的完整答案，让候选人能够专注于表达，从容应对 Meta 这样的顶尖公司面试。

如果你也在准备大厂的算法与系统设计面试，却不清楚如何拆题和应对各种边界，欢迎添加微信，即可领取北美面试求职通关秘诀。我们也有代面试，面试辅助，OA代写等服务助您早日上岸~