Code Question 1
Description
Data scientists at Amazon are working on a logistics optimization tool to arrange delivery routes based on existing route patterns.
A prototype algorithm takes in two integers, size and target_sum, and generates a sequence of size whose sum of elements equals target_sum, and the absolute values of the elements form a permutation of size size. The tool outputs the lexicographically smallest such sequence.
Given two integers, size and target_sum, return the lexicographically smallest sequence of integers such that
- The sum of its elements equals
target_sum. - The absolute values of its elements form a permutation of size
size.
Note:
A sequence of size integers is a permutation if it contains all integers from 1 to size exactly once.
For example:
[4, 1, 2, 5, 3]is a permutation.- But
[2, 2, 3, 4, 5]is not.
Lexicographical Order Note:
Given two permutations x and y, x is lexicographically smaller than y if there exists an index i where x[i] ≠ y[i], and for this smallest index i, x[i] < y[i].
This means that when comparing x and y element by element from the start, the first position at which they differ determines their order. If the element in x is less than the corresponding element in y at this position, x is considered smaller.
Example
Suppose size = 5, target_sum = 9
Some sequences of size 5 with sum 9 are:
| Sequence | Sum |
|---|---|
| [-1, -2, 3, 4, 5] | 9 |
| [-3, 1, 2, 4, 5] | 9 |
| [-2, 1, 3, 4, 5] | 9 |
| [-3, 1, 2, 5, 4] | 9 |
| [-3, 1, 2, 4, 5] | 9 |
Function Description
Complete the function findOptimalSequence in the editor below.
findOptimalSequence has the following parameters:
int size: the number of elements in the sequencelong int target_sum: the sum of elements in the sequence
Returns:
int[size]: the lexicographically smallest sequence of size integers that meets the criteria.- If it is not possible, return an array of size
size, filled with zeroes.
Constraints:
- 1 <= size <= 100000
- -6000000000 <= target_sum <= 6000000000
Sample Case 0
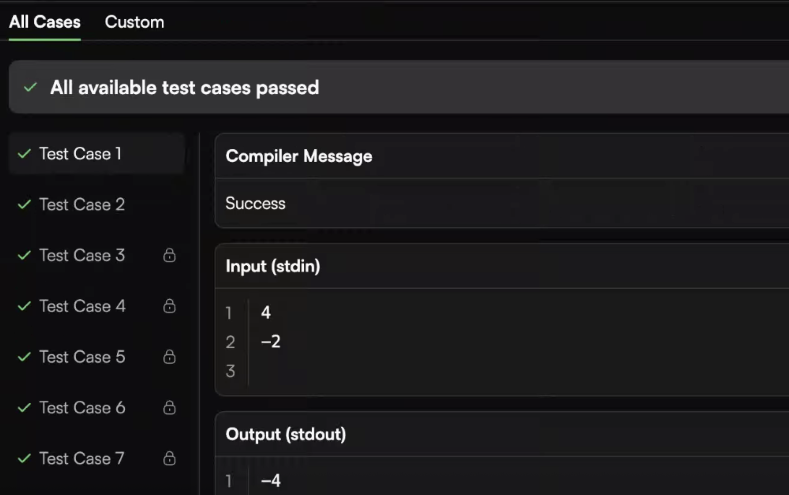
Input:
size = 4
target_sum = -2
Output:
-4
-2
1
3
Explanation:
Here size = 4 and target_sum = -2
Possible sequences with size = 4 and target_sum = -2 which also form a permutation, when absolute values of elements are taken, are:
- [-1, -2, -3, 4]
- [-3, 1, 2, 4]
- [-2, -4, 1, 3]
- [-4, -2, 1, 3] etc.
Code Question 2
Description
Returns:int: the number of subsequences of c that is lexicographically greater than s, modulo 10^9 + 7.
Constraints
- 1 <= |c| <= 100000
- 1 <= |s| <= 100
candsconsist of lowercase English letters
Function Description
Complete the function countSecurePasswordVariations in the editor below.
countSecurePasswordVariations has the following parameters:
string c: customer's passwordstring s: system-generated password
Returns:
int: the number of subsequences ofcthat is lexicographically greater thans, modulo 10^9 + 7.
Sample Case 0
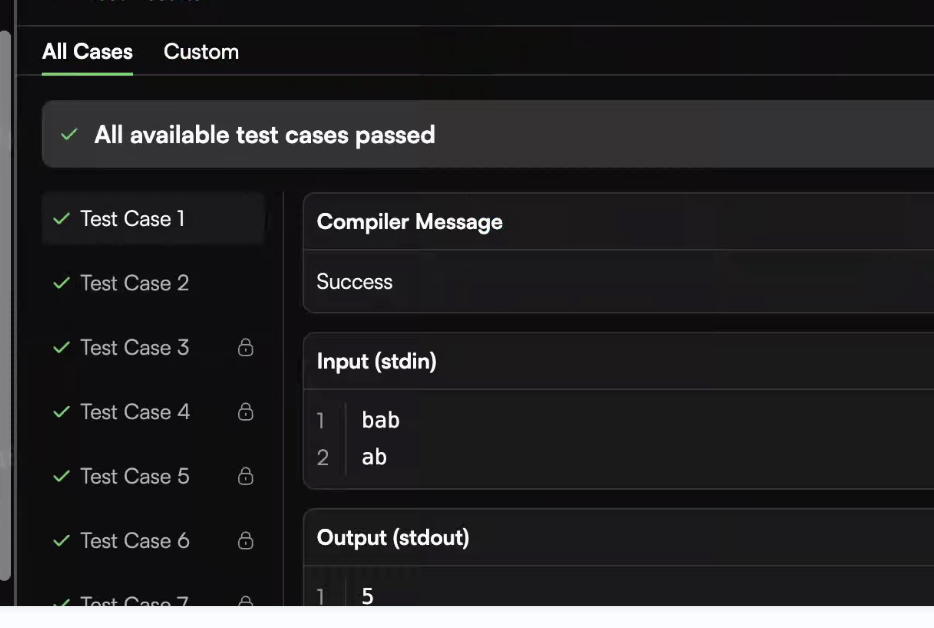
Input:
c = "bab"
s = "ab"
Output:
5
Explanation:
Let's examine all possible subsequences that can be derived from c = "bab" and compare them lexicographically with s = "ab":
| Subsequence | Lexicographical comparison with s |
|---|---|
| "b" | Greater |
| "ba" | Greater |
| "bb" | Greater |
| "bab" | Greater |
| "a" | Smaller |
| "ab" | Equal |
| "b" | Greater |
From all the subsequences of c, we find that:
- 1 subsequence is lexicographically smaller than
s("a") - 1 subsequence is lexicographically equal to
s("ab") - 5 subsequences are lexicographically greater than
s
So the answer is 5.
另一个例子:
Input:
c = "aba"
s = "ab"
Output:
3
Explanation:
Let's look at all possible subsequences that can be obtained from c:
| Subsequence | Lexicographical comparison with s |
|---|---|
| "a" | Smaller |
| "ab" | Equal |
| "aa" | Smaller |
| "aba" | Greater |
| "b" | Greater |
| "ba" | Greater |
| "a" | Smaller |
From all possible subsequences, 3 are lexicographically smaller, 1 is equal, and 3 are greater than s. Hence the answer is 3.
我们长期稳定承接各大科技公司如Capital One、TikTok、Google、Amazon等的OA笔试代写服务,确保满分通过。如有需求,请随时联系我们。
We consistently provide professional online assessment services for major tech companies like TikTok, Google, and Amazon, guaranteeing perfect scores. Feel free to contact us if you're interested.