Two Sigma 近期的OA 限时120分钟2道算法题，还是非常宽松的，我们一起看看真题吧~

1. IPO share allocation

An initial public offering (IPO) refers to the process of offering shares of a private corporation to the public in a new stock issuance. Public share issuance allows a company to raise capital from public investors. IPO process can go through a typical auction, and an IPO price is not set before the auction. Potential buyers are able to bid for the shares they want and the price they are willing to pay. The bidders who were willing to pay the highest price are then allocated the shares available.

Before the auction ends, potential buyers can submit bids containing: user Id, number of shares, bidding price, timestamp.
Once all the bids are submitted, the allotted placement is assigned to the bidders from the highest bids down, until all of the allotted shares are assigned. The auction assigns shares in multiple rounds until all shares are allocated or no more bids. In each round, it finds the bids with highest prices, assigns the shares, and removes the assigned bids:

1. If the bid (with the highest price) has only 1 bidders, the bidder gets shares he/she bids for (or get whatever left if the unallocated shares are less than the bid shares);
2. If the bids (with the highest price) have multiple bidders, the bidders are assigned shares as follows:
   Shares are distributed round robin style (i.e. one share per bidder in sequence until shares are all allocated) to bidders in the same price group, with the bidders sorted by timestamp. Once a bidder gets the number of shares they bid for, they will be removed from the above iterative process and the process which then continues until all bidders are removed or the shares get exhausted, whichever comes first.

Find out all bidders (user IDs) with no share allocation.

Function Description

Complete the function getResults in the editor below. The function must return a list of integers, each an Id for those bidders who receive no shares, sorted ascending.

getResults has the following parameter(s):
bids[bids[0],...,bids[n-1]]: a 2D array of arrays of integers, Id, shares, price, timestamp named u, sc, bp, ts going forward
totalShares: an integer, the total shares to allocate

Constraints

• 1 ≤ n < 10⁴
• 1 ≤ u, sc, bp, ts, totalShares < 10⁸

▼ Input Format For Custom Testing

▼ Sample Case 0

Sample Input 0

3  
4  
1 2 5 0  
2 1 4 2  
3 5 4 6  
3

Sample Output 0

3

Explanation 0
There are totalShares = 3 shares among the 3 bidders. The first 2 shares are allotted to the user with Id 1 as it has the highest bidding price. The 3rd share is allotted to the user with Id 2 as it is the first user, based on timestamp, in the bidding group having the bidding price 4. The only bidder who doesn’t receive shares has user Id of 3.

2. Question 2

A sewer drainage system is structured as a tree. Water enters the system at n nodes numbered from 0 to n-1 and flows through the tree to the root, which has the number 0. The tree structure is defined by an array parent, where parent[i] = j means that water flows from node i to its direct parent node j. Water exits the system after it flows through the root, so the root has no parent, represented as parent[0] = -1. The value in input[i] denotes the amount of water that enters the sewer system at node i. This excludes water that flows into i from its children. The total flow through a node is thus the flow that enters at that node, plus the sum of the total flows of all of its children.

Your task is to divide the system into two smaller pieces by cutting one branch so that the total flows of the resulting subtrees are as close as possible.

Example

parent = [-1, 0, 0, 1, 1, 2]  
input = [1, 2, 2, 1, 1, 1]

The structure of the system is shown in the diagram below. The nodes are labeled as <node number>/<input flow>.

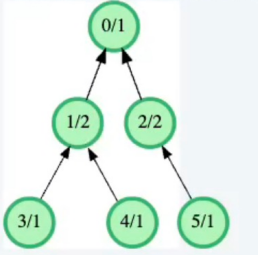
Cut the branch between nodes 1 and 0.
The partition {0, 2, 5} has total flow input[0] + input[2] + input[5] = 1 + 2 + 1 = 4.
The partition {1, 3, 4} has total flow input[1] + input[3] + input[4] = 2 + 1 + 1 = 4.
The absolute difference between the total flows of the two new sewer systems is 4 - 4 = 0.

Constraints

• 2 ≤ n ≤ 10⁵
• 1 ≤ input[i] ≤ 10⁴
• parent[0] = -1
• parent[i] < i for 1 ≤ i < n
• The depth of the tree is at most 500.

▼ Input Format Format for Custom Testing

▼ Sample Case 0

Sample Input

4 → parent[] size n = 4  
-1 → parent[] = [-1, 0, 1, 2]  
4 → input[] size n = 4  
1 → input[] = [1, 4, 3, 4]

Sample Output

2

Explanation
The structure of the system is shown in the diagram below.

The optimal value of 2 is achieved by cutting between nodes 1 and 2.
The resulting subtrees {0, 1} with total flow 1 + 4 = 5 and {2, 3} with total flow 3 + 4 = 7 differ by |5 - 7| = 2

我们长期稳定承接各大科技公司如Two Sigma、TikTok、Google、Amazon等的OA笔试代写服务，确保满分通过。如有需求，请随时联系我们。

We consistently provide professional online assessment services for major tech companies like TikTok, Google, and Amazon, guaranteeing perfect scores. Feel free to contact us if you're interested.