1. String Patterns
Given the length of a word (wordLen) and the maximum number of consecutive vowels that it can contain (maxVowels), determine how many unique words can be generated. Words will consist of English alphabetic letters a through z only. Vowels are v: {a, e, i, o, u}; consonants are c: the remaining 21 letters. In the explanations, v and c represent vowels and consonants.
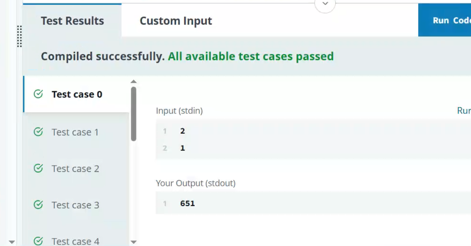
wordLen = 1
maxVowels = 1
Patterns: {v, c}
That means there are 26 possibilities, one for each letter in the alphabet.
V (5) or C (21)
wordLen = 4
maxVowels = 1
Patterns: {cccc, vccc, cvcc, ccvc, cccv, vcvc, cvcv, vccv}
There are 412,776 possibilities -- see below:
C C C C → 21 * 21 * 21 * 21
V C C C → 5 * 21 * 21 * 21
C V C C → 21 * 5 * 21 * 21
C C V C → 21 * 21 * 5 * 21
C C C V → 21 * 21 * 21 * 5
V C V C → 5 * 21 * 5 * 21
C V C V → 21 * 5 * 21 * 5
V C C V → 5 * 21 * 21 * 5
(5 * 21 * 5 * 21) + (21 * 5 * 21 * 5) + (5 * 21 * 21 * 5) = 3 * 11025 = 33075
194481 + 185220 + 33075 = 412776 possible solutions.
wordLen = 4
maxVowels = 2
In this case, all of the combinations from the previous example are still valid.
- There are 5 additional patterns to consider, three with 2 vowels (vcc, cvc, ccv) and 2 with 3 vowels (vvcv and vvvc).
- Their counts are 3 * (5 * 5 * 21 * 21) = 3 * 11025 = 33075
and 2 * (5 * 5 * 5 * 21) = 2 * 2625 = 5250. - The total number of combinations then is 412776 + 33075 + 5250 = 451101.
The result may be a very large number, so return the answer modulo (10^9 + 7).
Function Description
Complete the function calculateWays in the editor below.
2. Vowel Substring
Given a string composed of lowercase letters within the ASCII range 'a'-'z', determine the number of substrings that consist solely of vowels, where each vowel appears at least once. The vowels are ['a', 'e', 'i', 'o', 'u']. A substring is defined as a contiguous sequence of characters within the string.
Example
s = 'aeioaeaxaaeuiou'
There is a substring to the left that is made of vowels, aeioae which is followed by an x. Since x is not a vowel, it cannot be included in the substring, and this substring does not contain all of the vowels. It is not a qualifying substring. Moving to the right, there are four substrings that do qualify: aaeuiou, aeuiou, aeuio and aeuio.
Function Description
Complete the function vowelSubstring in the editor with the following parameter(s):
Parameters
string s: a string
Returns
int: the number of substrings that consist of vowels only (a, e, i, o, u) where every vowel appears at least once
Constraints
- 1 ≤ size_of(s) ≤ 10^5
- s[i] is in the range ascii['a'-'z'] (where 0 ≤ i < size_of(s))
Sample Case 0
Sample Input for Custom Testing
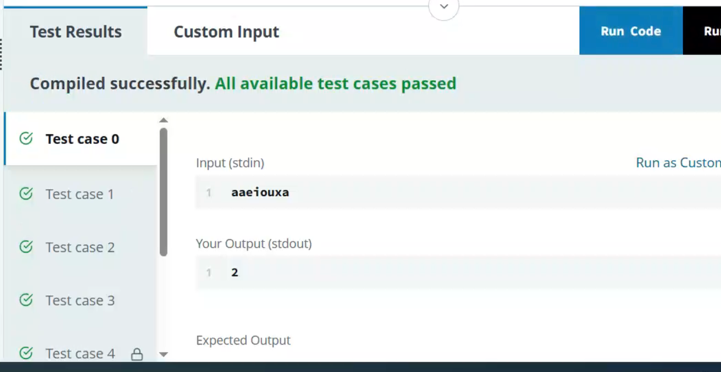
STDIN -> aaeioux a
Function -> s = "aaeoiuxa"
Sample Output
2
Explanation
s = "aaeoiuxa"
There are two qualifying substrings:s[0:5] = "aeoiu"s[1:5] = "eoiu"
3. Maximum Order Volume
During the day, a supermarket will receive calls from customers who want to place orders. The supermarket manager knows in advance the number of calls that will be attempted, the start time, duration, and order volume for each call. Only one call can be in progress at any one time, and if a call is not answered, the caller will not call back. The manager must choose which calls to service in order to maximize order volume. Determine the maximum order volume.
Example
start = [10, 5, 15, 18, 30]
duration = [30, 12, 20, 35, 35]
volume = [50, 51, 20, 25, 10]
The above data as a table:
| Caller | Start time | Duration | Order volume |
|---|---|---|---|
| 1 | 10 | 30 | 50 |
| 2 | 5 | 12 | 51 |
| 3 | 15 | 20 | 20 |
| 4 | 18 | 35 | 25 |
| 5 | 30 | 35 | 10 |
The fourth call will start at time = 18, and last until time = 53.
The fifth call will start at time = 30, and last until time = 65.
The first call completely overlaps the second and third calls, and partially overlaps the fourth and fifth calls. Choosing calls that do not overlap, and answering the 2nd and 4th calls leads to the maximum total order volume of 51 + 25 = 76.
Function Description
Complete the function phoneCalls in the editor below.
phoneCalls has the following parameter(s):
int start[n]: the start times of each callint duration[n]: the durations of each callint volume[n]: the volumes of each order
Returns
int: the maximum possible volume of orders that can be received
Constraints
- 1 ≤ n ≤ 10^5
- 1 ≤ start[i] ≤ 10^9
- 1 ≤ duration[i] ≤ 10^9
- 1 ≤ volume[i] ≤ 10^3
Sample Case 0
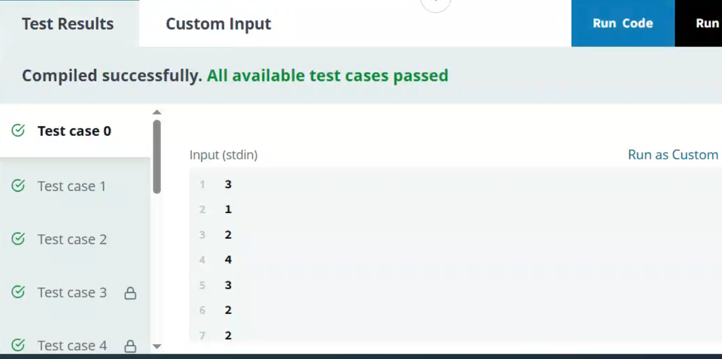
Input
start[] = [1, 2, 4]
duration[] = [2, 2, 1]
volume[] = [1, 2, 3]
Sample Output
4
Explanation
The calls happen in the intervals:
[1, 3],
[2, 4],
[4, 5]
The first and third calls together make up the order volume 4, and their intervals do not intersect.
The first and second calls intersect, as do the second and third calls. Only one call from either of these pairs can be serviced. The most efficient calls to answer are the first and third, with a total volume of 4.
我们长期稳定承接各大科技公司如TikTok、Google、Amazon等的OA笔试代写服务,确保满分通过。如有需求,请随时联系我们。
We consistently provide professional online assessment services for major tech companies like TikTok, Google, and Amazon, guaranteeing perfect scores. Feel free to contact us if you're interested.
