会改一些数值,人物名字,还有具体问题,所以大家答题的时候还是要注意细节
Question 1
Donald and Goofy plan to meet at a theatre, but will each independently arrive at a uniformly random time between 18:00 and 19:00. Donald will only wait 12 minutes for Goofy before leaving, but Goofy is willing to wait 36 minutes for Donald before leaving. What is the probability they end up meeting each other?
For integer answers, please input your answer in the first blank and input the integer 1 in the second blank.
For fraction answers, please input your numerator in the first blank and your denominator in the second blank. Answers should be expressed in simplest form as improper fractions if applicable.
Question 2
A dog is playing in a swamp as shown in the diagram. She runs at 3 m/s in the swamp (anywhere except the road) and 5 m/s on the road. She got hungry and decided to return home imminently. What is the shortest possible amount of time (in seconds) it would take for her to go home?
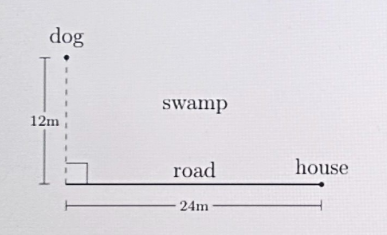
For integer answers, please input your answer in the first blank and input the integer 1 in the second blank.
For fraction answers, please input your numerator in the first blank and your denominator in the second blank. Answers should be expressed in simplest form as improper fractions if applicable.
Question 3
Iggy is tiling the floor with black and white tiles. Every turn she draws a tile from an unlimited pool of black and white tiles and places it on the floor. Given that the probability of drawing black tiles is 3, compute the expected number of turns it would take for her to place two black tiles consecutively.
For integer answers, please input your answer in the first blank and input the integer 1 in the second blank.
For fraction answers, please input your numerator in the first blank and your denominator in the second blank. Answers should be expressed in simplest form as improper fractions if applicable.
Question 4
Aaron, Bryce, and Craig are all distinct integer ages. They had the following conversation:
- Bryce to Craig: You're the youngest one.
- Aaron to Bryce: Your age is exactly 70% greater than mine.
- Aaron to Craig: Your age is the average of my age and Bryce’s age.
- Craig to Aaron: I’m at least 8 years older than you.
However, not all of these statements are true. When speaking to someone older, the speaker always tells the truth. Otherwise, when speaking to someone younger, the speaker always lies. How old is Craig?
Please express your answer as an integer.
Question 5
Consider a fair 12-sided die (i.e., a discrete random variable uniformly distributed on the integers {1,2,...,12}). Roll the die 10 times. Let X be the number of rolls that are divisible by 4. Calculate E[X].
For integer answers, please input your answer in the first blank and input the integer 1 in the second blank.
For fraction answers, please input your numerator in the first blank and your denominator in the second blank. Answers should be expressed in simplest form as improper fractions if applicable.
Question 6
Three real numbers are chosen from the interval U[0, 4] independently and uniformly at random. What is the probability that the largest number is between 0.5 and 1?
For integer answers, please input your answer in the first blank and input the integer 1 in the second blank.
For fraction answers, please input your numerator in the first blank and your denominator in the second blank. Answers should be expressed in simplest form as improper fractions if applicable.
Question 7
A picnic table is covered with a 3 by 3 grid of squares. Two of the squares are black and the rest are white. How many ways can you place 2 apples and 1 orange such that at least one item is on a black square? Assume that at most one item can be placed in each square and the apples are indistinguishable.
Please express your answer as an integer.
Question 8
A toad is trying to get from point A to point B without overshooting, but he can only move up or right. He always alternates his step sizes between moving 1 unit in a single direction and moving 3 units in a single direction. Compute the number of ways the toad can start at point A and end at point B.
- A(0,0)
- B(13,4)
Please express your answer as an integer.

Question 9
Three biased coins all have different chances of landing heads. The most biased coin lands on heads with probability 910109, the least biased coin lands on heads with probability 11202011, and the remaining coin lands on heads with probability 4554. I picked a coin uniformly at random to flip and it landed on tails. What is the probability that I picked the most biased coin?
For integer answers, please input your answer in the first blank and input the integer 1 in the second blank.
For fraction answers, please input your numerator in the first blank and your denominator in the second blank. Answers should be expressed in simplest form.
我们提供OA代写服务,代面试服务,面试辅助服务等。对于OA代写我们将确保你获得满分,联系我们立即进行预约。
We provide services for writing online assessments (OA), proxy interviews, and interview assistance. For the OA writing service, we will ensure that you achieve a perfect score. Contact us now to make an appointment.
